Density Estimation
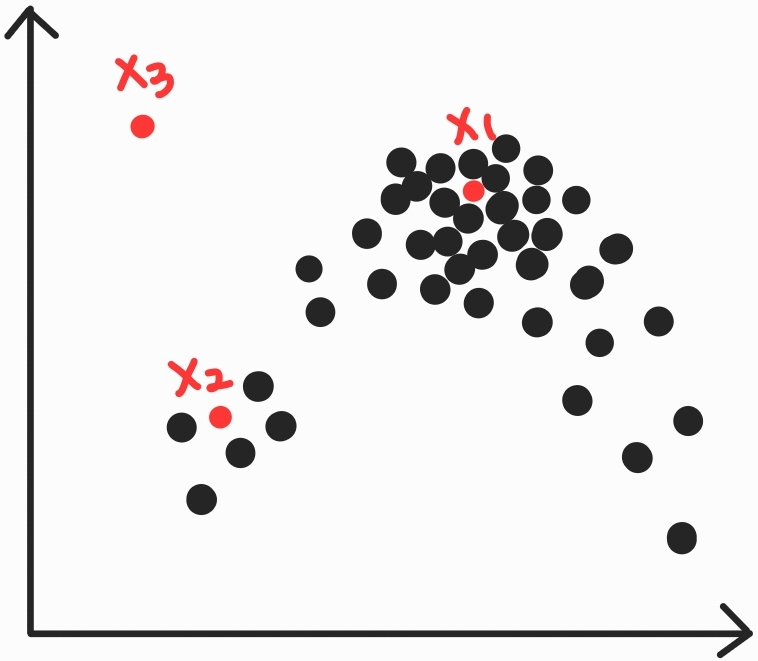 |
밀도추정이란, 어떤 점 x에서 데이터가 발생할 확률, 즉 확률분포 $P(x)$를 구하는 문제이다. 예를들어 현재와 같은 분포에서는 $P(x_1)>P(x_2)>P(x_3)$이겠다. $x_1$쪽에는 밀집된만큼, 발생할만하고 $x_3$쪽에는 전혀 없어 발생가능성이 현저히 적다. |
분포를 어떻게 구하냐에 따라서 다음과 같이 나뉜다.
- Parametic Methods(단순한 분포를 가정하고 유한한 파라미터를 구하자)
- ML(Maximum Likelihood) Estimation
- MAP(Maximum A Posteriori) Estimation
- Non-Parametic Methods(복잡한 분포를 가정하자)
Parametic Methods
우리는 평균과 분산값 이렇게 두 가지만 있으면 가우시안 분포를 그려낼 수 있다.
이와 같이 유한한 파라미터로 그릴 수 있는 분포를 따른다고 깔고가는 것이다.
그렇게 다른 파라미터 값을 세팅해서 분포를 만들어냈을 때 어떤 것이 더 수학적으로 잘 나타냈느냐를 표현해보자.
$X = \left\{x_1, x_2, \cdots , x_n \right\}$일 때
가우시안같은 단순한 확률분포 $P(X|\theta)$를 따른다고 가정하고
$P(X|\theta)$를 결정하기 위한 파라미터 $\theta$를 구한다.
어떤 $\theta$를 설정해야 주어진 데이터 $X$를 잘 표현할 수 있을까?
파라미터 추정 방법으로 ML Estimation과 MAP Estimation가 있다.
ML(Maximum Likelihood) Estimation
다음과 같이 샘플이 6개가 있다.
분산은 일정하고 평균이 다른 $\theta_1, \theta_2$ 가우시안 분포 두개를 그렸다고 하자.
이때 어떤 분포가 더 데이터를 잘 설명했는가?

직관적으로 딱봐도 $\theta_1$ 분포가 데이터 $X$를 잘 설명하였다.
그렇다면 이를 수식적으로 표현해보자.
주어진 데이터셋 $X = \left\{x_1, x_2, \cdots , x_n \right\}$가 최대로 관측될 수 있는 파라미터 $\theta$를 찾는다.
즉 likelihood를 최대화하는 파라미터를 찾는다.
$$\hat{\theta} = \textrm{arg } \underset{\theta}{max}P(X|\theta)$$
보통 sample 간에는 독립적이므로
$$P(X|\theta) = P(x_1, x_2, ..., x_n|\theta) = P(x_1|\theta)P(x_2|\theta)...P(x_n|\theta)=\prod\limits_{i=1}^{n}P(x_i|\theta)$$
1 이하의 값을 지니는 확률값을 계속 곱하게 된다면 점점 0과 가까워지면서 사라지겠다.
그래서 log를 붙여주어서 곱셈을 덧셈으로 바꾸는 전략을 사용한다.
$$L(\theta) = log P(X|\theta) = log\left\{P(x_1|\theta)P(x_2|\theta)\cdots P(x_n|\theta) \right\} = \sum\limits_{i=1}^{n}log P(x_i|\theta)$$
정규분포로부터 {$x_1, x_2, \cdots, x_n$} n개를 표본 추출했을 때
이들로부터 가우시안 분포의 평균 $\mu$와 분산 $\sigma^2$는 외워서 알고 있다.
우리가 익히 고등학생 때 배운 모평균의 추정값은
$$\hat{\mu} = \frac{1}{n}\sum_{i=1}^{n}x_i$$
모분산의 추정값은
$$\hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^{n}\left(x_i-\mu\right)^2$$
이를 Maximum Likelihood로 구해보고 확인하자.
$$\frac{\partial L(\theta)}{\partial \mu}
=\frac{1}{\sigma^2}\sum_{i=1}^{n}(x_i-\mu) = \frac{1}{\sigma^2}\left(\sum_{i=1}^{n}x_i-n\mu\right) = 0$$
$$\frac{\partial L(\theta)}{\partial \sigma} =-\frac{n}{\sigma}+\frac{1}{\sigma^3}\sum_{i=1}^{n}\left(x_i-\mu\right)^2 = 0$$
결국 미분값이 0이되는 지점을 찾아서 말그대로
"최대 우도"(Maximum Likelihood)를 만들어주는 모평균과 모분산을 표본으로부터 추정하는 것이다.
MAP(Maximum A Posteriori) Estimation
- Prior Probability(사전확률) $P(\theta)$ : 파라미터 $\theta$가 정답일 확률
- Posterior Probability(사후확률) $P(\theta|x)$ : 샘플 X가 발생(관측) 시 $\theta$가 정답일 확률
- $P(\theta|X) = \dfrac{P(X|\theta)P(\theta)}{P(X)}$
이때 $\theta$를 바꾼다고 $P(X)$값에 영향을 미치지는 않는다.
그러므로 $P(X|\theta)P(\theta)$를 최대화하는 $\theta$를 찾으면 되겠다.
$$\hat{\theta} = \textrm{arg } \underset{\theta}{max}P(\theta|X) = \textrm{arg } \underset{\theta}{max}P(X|\theta)P(\theta)$$
MLE와 같이 각 샘플 $x_i$ 발생 확률이 보통은 서로 독립적이라 다음의 특성을 사용한다.
$$P(X|\theta) = P(x_1, x_2, ..., x_n|\theta) = P(x_1|\theta)P(x_2|\theta)...P(x_n|\theta)=\prod\limits_{i=1}^{n}P(x_i|\theta)$$
그러면 MLE에 $logP(\theta)$ 항이 더 붙은 꼴로 나온다.
$$logP(X|\theta)P(\theta) = logP(X|\theta) + logP(\theta) = \sum\limits_{i=1}^nlogP(x_i|\theta) + logP(\theta)$$
결국 여기서 알 수 있는 것은 사전확률 $P(\theta)$의 영향에 따라서 MLE와 MAP의 결과가 같을 수도, 다를 수도 있다.

데이터와 MLE 혹은 MAP 방법을 통해서 모델에 사용되는 파라미터 $\theta$를 구할 수 있다.
이때 MLE는 관측된 데이터만을 이용하여 최대가 되게 하고,
MAP는 관측된 데이터 뿐 아니라 사전확률을 통해서 편향된 데이터에 대하여 대응을 해준다.
그렇기 때문에 사전확률만 제대로 알 수만 있다면 MAP가 올바른 decision이라고 말할 수 있겠다.
'딥러닝기초' 카테고리의 다른 글
| [Density Estimation]K-Nearest Neighbors Estimation과 Classification (0) | 2022.04.27 |
|---|---|
| [Density Estimation]파젠창(KDE)으로 파라미터 추정 (0) | 2022.04.26 |
| [확률]조건부 확률부터 Bayes Rule과 Bayes' Theorem 정리 (0) | 2022.04.23 |
| 딥러닝에서 사용하는 가우시안 분포 기초개념 (0) | 2022.04.22 |
| 분산부터 공분산행렬까지 (0) | 2022.04.21 |



