[SVD]Singular Value Decomposition와 고유치 및 고유벡터

PCA : input들의 공분산을 분해하여 데이터의 분포를 가장 잘 설명하는 최대 분산 축을 찾음.

input들의 공분산을 분해하여 데이터의 분포를 가장 잘 설명하는 k개의 축을 파악

SVD : 행렬 자체를 분해. 정방 행렬이 아니어도 가능함

PCA를 설명하면서 간단하게 고유치, 고유벡터의 정의를 살펴보았다.

 n x n의 행렬로부터 고유치와 고유벡터 n개의 열벡터를 모아 행렬 $V$로 나타내면 다음과 같이 $\lambda$가 대각성분을 지니게끔 할 수 있다. 

 

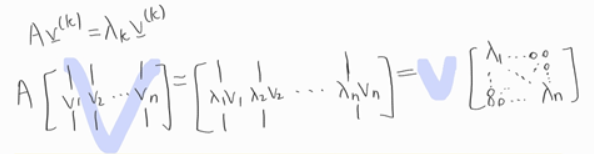
그렇게 나타낼 수 있는 이유가 아래에 제시되어있다. 위와 같이 나타낼 수 있도록 하는 trick이다. 

 

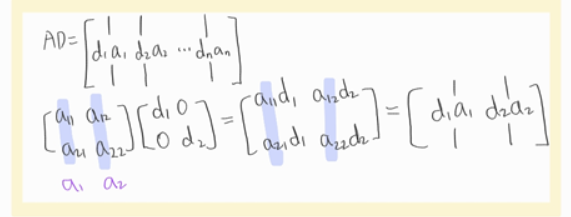
그러므로 우리는 위를 통해서 $AV = VD$로 표현 가능하고 이는 곧

$A=VDV^{-1}$

이를 Eigen-Decomposition 라고 부른다.

 

이와 같은 행위의 의의는 A matrix를 고유값, 고유벡터를 통해 표현가능하다는 점이다.

 

 

---

 Eigen-Decomposition에서 조금만 더 들어가보자.

$A=VDV^{-1}$에서 A가 symmetric matrix일 때 조금 더 특별한 성질이 있다.

결론부터 말하자면 $A=VDV^T$가 되는데, 보다시피 유일한 다른 점은 $V^{-1}$가 $V^T$로 치환된다는 점이다.

즉 $V^{-1} = V^T$이라는 것이고 이는 곧 직교행렬의 정의와 같다.

 

(직교행렬의 정의 : $V \cdot V^T = I$)

 

 직교행렬의 특성은 어떠한 $V_i$와 $V_j$ 간 orthogonal하기에 내적하면 0값을 갖는다.  

 

---

이제 SVD에 대한 이야기를 해보자.

기존 Eigen-Decomposition은 nxn의 정방행렬에 관해서 적용 가능했었고 또 그렇다고 모든 정방행렬이 가능한 것도 아니었다. 그러나 Singluar Value Decompostion은 다르다. 정방행렬이 아닌 m x n에 대해서도 적용 가능하다.

 

우선 SVD의 모양은 다음과 같다.

$A = U \Sigma V^T$

$U$ : m x m 직교행렬 ($AA^T$)

$\Sigma$ : m x n 직사각 대각행렬(Singular Value)

$V$ : n x n 직교행렬 ($A^TA$)

 

* $A^TA$와 $AA^T$는 A가 어떠한 행렬이든지 모두 대칭행렬(symmetric matrix)이 나온다.

* $A^TA$와 $AA^T$의 각각의 고유치는 일치하게 나온다. 

대각원소가 정확히 나타내는 것은 $A^TA$와 $AA^T$의 eigen-value들이 square root 값이다. 

* 크기가 큰 값부터 $\sigma_1, \sigma_2, ...$등이 된다. 크기가 클 수록 중요도도 크다.

 

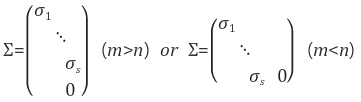
그럼 이렇게 분해한 게 뭐가 좋은 걸까? 활용에 대해 알아보자.

아래 그림은 m>n일 때의 모양이다. 

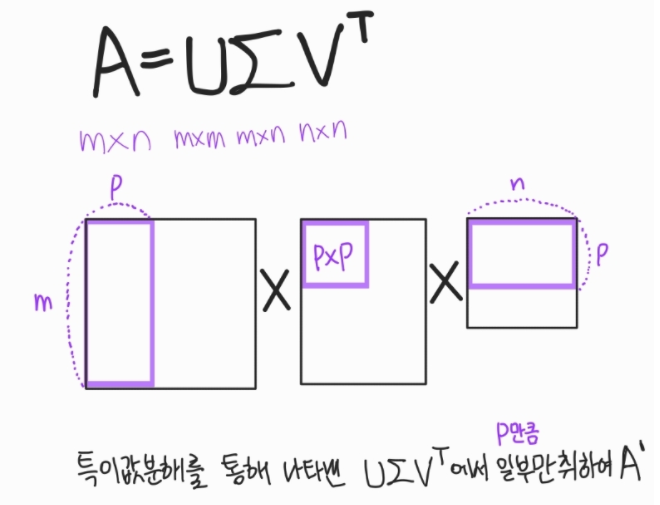
이때 완전한 A를 사용하는 것이 아니라 일부만 취하여 A'를 생성하면 데이터를 압축하는 효과가 나타난다.

 

 

아래는 p=2 즉 두 개의 singular value만 취했을 때를 나타낸다.

 

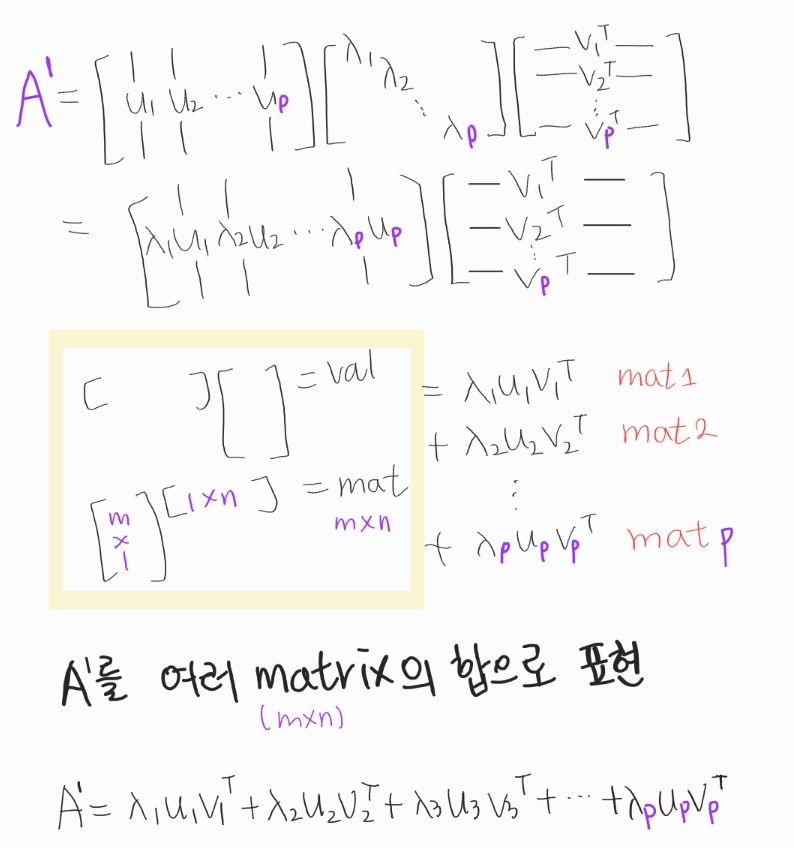
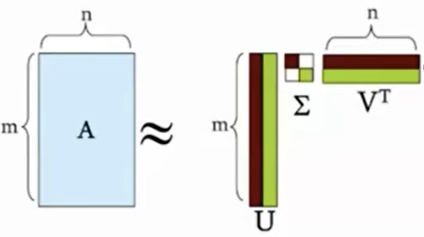
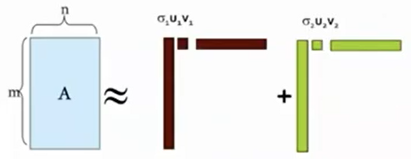
SVD로 데이터 압축된 모습

실질적인 singular value 개수에 따라 데이터가 압축된 형태를 살펴보자.

1개

5개

13개

그 이상