Decision Boundary
선형을 거쳐 나온 $w^Tx$에 아래와 같은 activation function을 거치면
그 값이 threshold보다 크냐 작느냐에 따라서 결과가 달라진다.
아래에서는 세로축을 기준으로는 빨간 x인 0과 0.5가 threshold인 상황이다.

두 함수 공통적으로 가로축 기준 $z=w^Tx$값이 0보다 크냐 작냐로도 이야기할 수 있겠다.
즉 $z=w^Tx = 0$이 결정적인 순간이 된다.
Decision Boundary is,
$d(x) = w^Tx = 0$

2차원의 feature space에서 1차원 직선의 boundary가 그려지듯이,
항상 n차원의 feature space에서 n-1차원의 boundary가 그려진다.
이 decision boundary를 hyperplane(초평면)이라고도 일컫는다.
또한 boundary를 만족하는 x들의 집합과 weight vector인 w와 orthogonal한 특징을 보인다.
(평면의 방정식을 생각할 때 법선벡터를 가지고 표현했던 것을 상기하면 된다)
Sample과 Decision boundary의 거리 구하기
어떤 직선 $d(x) = 2x_1 + x_2 - 4 = 0$과 점 x*(2, 4) 간의 거리를 구할 때
$$h = \frac{|2 * 2 + 1 * 4 - 4|}{\sqrt{2^2 + 1^2}} = \frac{4}{\sqrt{5}} = \frac{d(x^*)}{||w||_2}$$
위와 같이 구했다.
decision boundary의 어떤 sample 간의 거리를 구하는 식으로 아래를 기억하자.
$$h = \frac{d(x^*)}{||w||_2}$$
What is Margin?
우리가 동그라미와 세모를 구분지을 때 다음과 같이 세가지 직선으로 구분짓는다 하자.
이때 검정색은 아래에 볼 수 있듯이 너무 아슬아슬하게 구별한다.
그러나 빨간색은 여유롭게 구분해낸다.
눈으로 봐도 빨간색 선이 더 좋은 직선이라고 말할 수 있겠다.
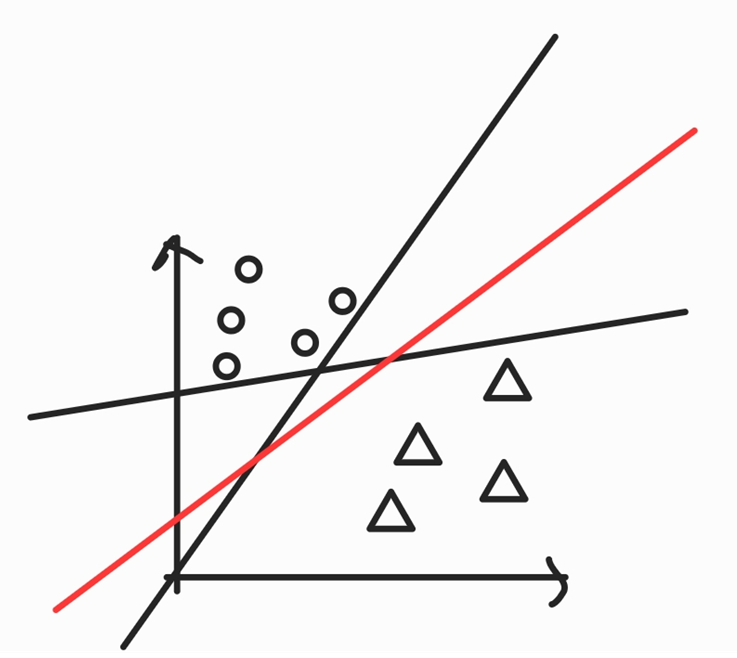
그러나 검정 직선들이나, 빨간 직선이나 오분류한 것이 없으므로 error 계산시 똑같이 0이 나오겠다.
그러면 아슬아슬 말고 빨간색 선처럼 넉넉한 마음으로 넉넉하게 구분 가능한 선을 어떻게 찾을 수 있을까?
이때 Margin이라는 개념이 나온다.
양쪽 class에 대한 여백(Margin)을 최대화 할 수록 더 좋은 분류기라고 말할 수 있을 것이다.
그렇다면 이 Margin이라는 여백을 어떻게 수학적으로 표현할까?
1) 직선과 제일 가까운 class마다 점을 choose
2) 점과 boundary 사이 거리를 최대화
또 여백을 최대로 하는 결정 초평면을 어떻게 찾을 것인가?
이때 Constrained optimization problem이 나온다.
SVM이 바로 여백을 최대로 하는 결정 초평면을 구하는 알고리즘이다.

선형 분리가 가능한 분류 문제를 생각하자.
분할 띠의 너비 2s를 여백(margin)이라고 부른다.
분할 띠의 경계에 있는 샘플 벡터를 support vector라고 부른다. 보라색에 해당되고
$d(x)= 1 or -1$이 각 클래스의 support vector로 설정하였다.
$d(x)\geq 1$이 ○이 있는 곳, $d(x)\leq -1$이 ●이 있는 곳에 해당된다.
x는 당연히 support vector일 때이고
$$Margin = 2s = \frac{2|d(x)|}{||w||_2} = \frac{2}{||w||_2}$$
margin을 가장 크게 하는 초평면의 기울기$(w)$를 찾는 것이 목적이다.
$$maximize : J(w) = \frac{2}{||w||_2}$$
이에 대한 제약조건은
$$w^Tx_i + b \geq 1, ∀y_i =1$$
$$w^Tx_i + b \leq -1, ∀y_i =-1$$
이 제약조건을 한방에 써보자.
$$y_i(w^Tx_i + b)-1\geq 0, i=1,2, ... , n$$
$$\textrm{minimize } J(w) = \frac{1}{2}||w||_2^2$$
$$\textrm{subject to } y_i(w^Tx_i + b)-1\geq 0, i=1,2, ... , n$$
근데 여기서 훈련 샘플 개수 n개 만큼의 제약조건 식이 세워지는 것이다.
아니.... 이걸 어떻게 푼담.......^^ 다음 시간에 계속!
'딥러닝기초' 카테고리의 다른 글
| 커널함수와 함께하는 Non linear SVM (0) | 2022.04.11 |
|---|---|
| 선형 SVM까지 끝장보기 (0) | 2022.04.09 |
| Constraint Optimization와 같이 정리하는 KKT condition (0) | 2022.04.04 |
| [SVD]Singular Value Decomposition와 고유치 및 고유벡터 (0) | 2022.03.18 |
| [PCA] 고유치, 고유벡터의 대표적인 활용 (0) | 2022.03.15 |



