역행렬부터 시작하자.
$n \times n$ 행렬 A의 역행렬 $A^{-1}$을 정의하면
$$A^{-1}A = AA^{-1} = I$$
역행렬은 언제 존재하는가?
$A^{-1}$ exists $\Leftrightarrow Ax \neq 0$ for all $x \neq 0 \Leftrightarrow N(A) = 0$
Nullspace
$N(A) = \left\{x|Ax = 0\right\}$
A에 x를 곱했을 때 0으로 보내는 x들의 집합
즉, 역행렬이 존재하는 조건은 A에 x를 곱했을 때 0으로 보내는 x vector가 영벡터 뿐일 때를 뜻한다.
A의 역행렬이 존재한다는 말은 곧 A가 invertible하다, A가 non-singular하다와 동치이다.
반대로 A의 역행렬이 존재하지 않는다는 말은 곧 A가 non-invertible하다, A가 singular하다와 같은 말이다.
또한 A가 역행렬을 갖기 위해서는 full rank이어야 한다.
n x n 행렬인 경우 rank(A) = n어야 하고
이는 곧 column끼리, row끼리 linearly independant하다는 것이다.
역행렬이 존재하지 않는 경우를 살펴보자.


행렬식(Determinant)
행렬식의 본래 정의는 row vector의 선형 결합이다.
$$S = \left\{ v \in \mathbb{R}^n : v= \sum_{i=1}^n\alpha_ia_i,\textrm{ where } 0\leq \alpha_i\leq 1, i = 1, \cdots ,n \right\}$$
2개의 벡터로의 선형결합으로는 평행사변형의 면적을 나타낸다.
벡터가 3개라면 det A 는 부피가 되겠다.
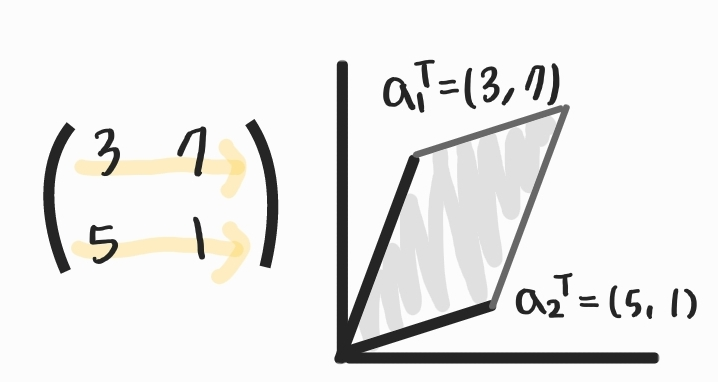

여기서 주목할만한 점은 아까 위에서 역행렬이 존재하지 않는 행렬인 경우 평행사면형이 그려지지 않는다.
이말인 즉슨 이때의 행렬식 결과(평행사변형의 면적)는 0이 된다.
det A = 0 $\Leftrightarrow$ A의 역행렬이 존재하지 않는다.
결국 행렬식 값이 0이라는 것은
1) 역행렬인 존재하지 않기도 하고,
2) full rank가 아니기도 하고,
3) row끼리 혹은 col끼리 선형독립이 아닌 것이 하나라도 존재한다는 뜻이다.
Properties
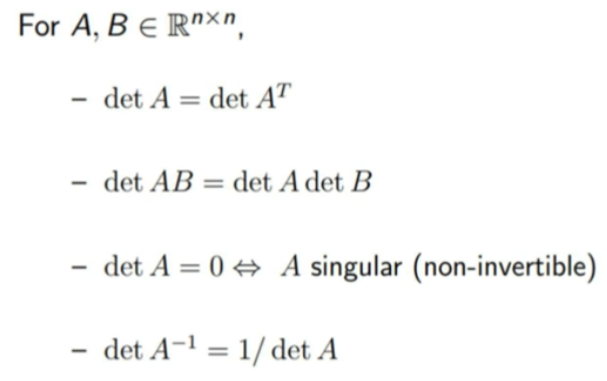
이제 고유치와 고유벡터를 보자.
n x n인 A matrix가 있을 때
$$Ax = \lambda x, x \neq 0$$
을 만족하면 $\lambda$는 고유치, $x$는 고유벡터라고 부른다.
x vector을 A로 선형변환하여 어디로든 뻗어나갈 수 있는데
어쩌다 그 결과가 해당 벡터의 $\lambda$배가 되는 벡터인 것이다.
위의 식을 다시 쓴다면
$$(\lambda I - A)x = 0, x \neq 0$$
$(\lambda I - A)$의 역행렬이 만약 존재한다면 x vector는 0 vector가 된다.
그러나 x는 영벡터가 아닌 경우만 해당되기 때문에 $(\lambda I - A)$의 역행렬은 존재하지 않아야 한다.
여기서 자연스럽게 고유치와 고유벡터를 구하는 방법을 구해낼 수 있는데
방금 위에서 A의 역행렬이 존재하지 않는다는 것은 det A = 0을 만족하였다.
그러므로 우리는 고유치, 고유벡터를 구하기 위해서
$$|\lambda I - A| = 0$$
이 행렬식을 풀어내면 $\lambda$에 관한 식이기 때문에 고유치를 구할 수 있게 된다.
2 x 2의 고유치, 고유벡터를 구하는 예시이다.
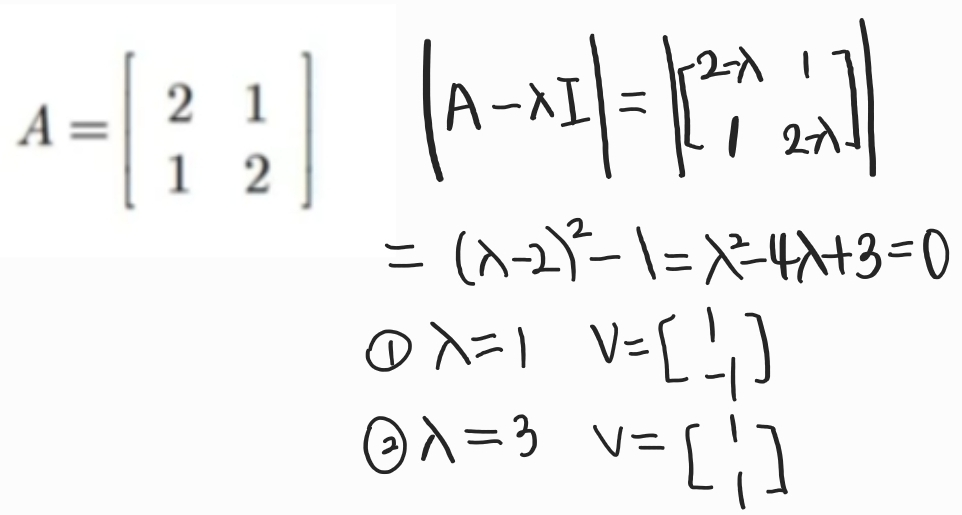
Properties
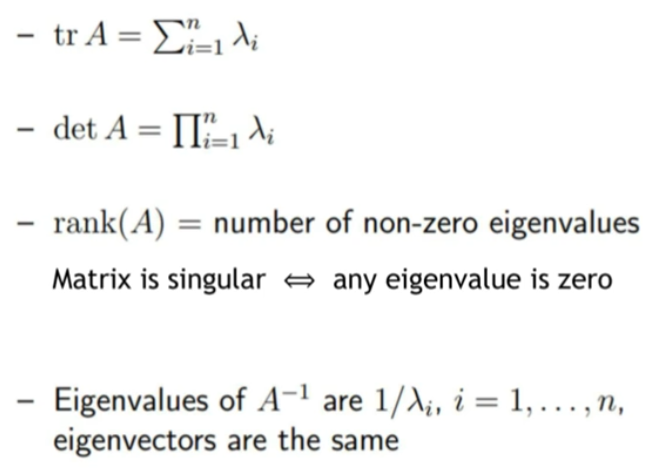
'딥러닝기초' 카테고리의 다른 글
| Conv1D의 기본적인 input과 output (1) | 2023.01.18 |
|---|---|
| Logistic Regression과 비용함수 알아보기 (0) | 2022.06.02 |
| [Density Estimation]GMM(Gaussian Mixture Model)과 EM 알고리즘 (0) | 2022.04.28 |
| [Density Estimation]K-Nearest Neighbors Estimation과 Classification (0) | 2022.04.27 |
| [Density Estimation]파젠창(KDE)으로 파라미터 추정 (0) | 2022.04.26 |



