명칭은 Logistic Regression이지만 사실은
Linear regression 문제를 확장하여 최종 목적은 Classification 하기 위함이다!
Binary Classification 문제에서,
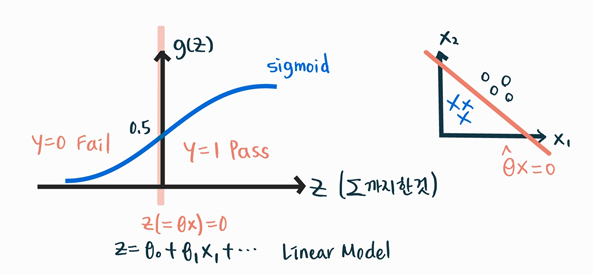
어떤 대학 과목이 Pass/Fail로 학점을 줄 때 Pass면 1, Fail이면 0으로 나타낼 수 있을 것이다.
출석, 과제 등과 같은 feature, (온라인 강의니까 널널하게 pass를 주겠다와 같은)교수님의 bias까지 모두 고려하여 합한다. ( $\theta^Tx$ )
시그모이드 함수를 거쳐 $\theta^Tx$이 무엇이 나오던지 0과 1 사이 값으로 바꾼다. 다른 시각으로는 1이 될 확률로 볼 수 있겠다. ( $\sigma(\theta^Tx)$ )
보통은 0.5 이상이면 P, 그 이하면 F를 부여받겠다.
if $\sigma(\theta^Tx)\geq0.5$, y=1 Pass
if $\sigma(\theta^Tx)<0.5$, y=0 Fail
Decision Boundary
Decision boundary란 feature space에서 각 클래스를 결정 짓는 경계이다.
위의 예시에서는 decision boundary는 $h_{\theta}(x) = \hat{\theta}^{T}x=0.5$으로, P와 F가 구분되는 경계이다.
최적의 $\hat{\theta}$를 찾았다면, $h_{\theta}(x) = \hat{\theta}^{T}x = 0$이되는 경계가 확실한 Decision boundary가 되겠다.
Logistic Regression Model
Linear Model
$z = \theta^Tx = \theta_0 + \theta_1x_1 + ... + \theta_nx_n = \sum_\limits{i=0}^n\theta_ix_i$
Sigmoid Function
$y = h_{\theta}(z) = \sigma(z) = \dfrac{1}{1+e^{-z}}$
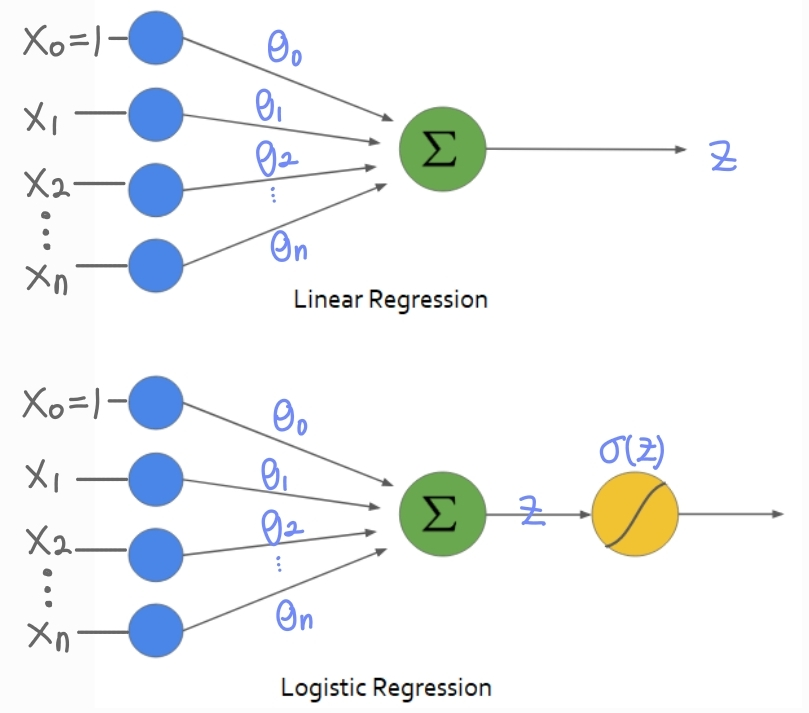
원래 했던 그대로 Linear model을 사용하는 대신,
마지막 sigmoid function만 씌워주어 output이 [0, 1] 값으로 나오게 하는 것이다.

Loss Function
Linear Regression에서는 Mean Square Error를 썼다.
그러나, Logistic Regression에서는 MSE를 사용할 수 없다.
왜냐하면 cost function을 그렸을 때 convex하지 않아서 local minimum이 자주 발생한다.
그럼 어떤 cost function을 쓰느냐, 바로 Cross Entropy Loss이다.
이는 당연하게도 cost function이 convex하다.
Cross Entropy Loss
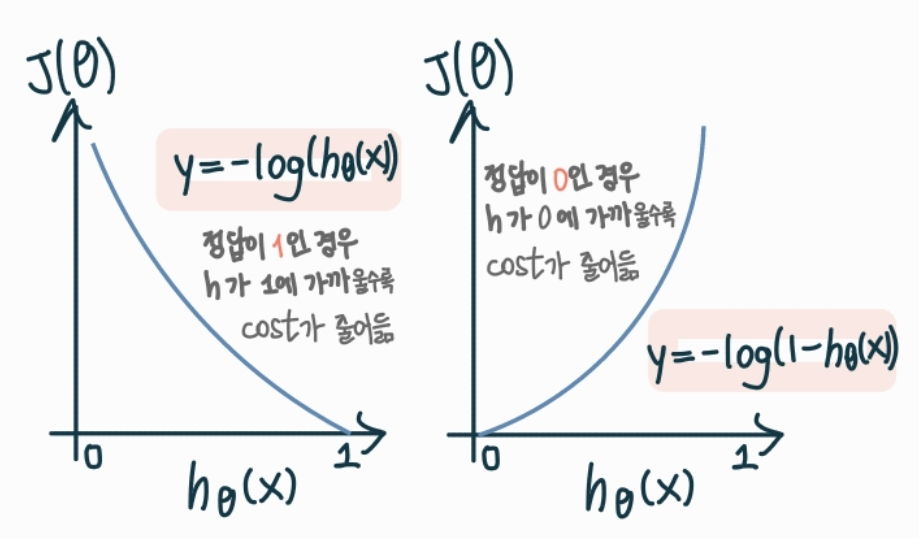
$J(\theta) = \dfrac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}, y^{(i)})$
Cost$(h_{\theta}(x), y) = -log(h_{\theta}(x))$ if y = 1
Cost$(h_{\theta}(x), y) = -log(1-h_{\theta}(x))$ if y = 0
Cross Entropy Loss의 미분
신기하게도 Linear Regression의 Gradient Descent와 동일한 식이 나온다.
분명 loss function을 다르게 정의했는데 말이다.
$$\dfrac{\partial }{\partial \theta _j}J(\theta) = \frac{1}{m}\sum^m_{i=1}\left [ h_\theta(x^{(i)})-y^{(i)} \right ]x_j^{(i)}$$
단, Linear Regression 에서는 가설함수 $h_{\theta}(x) = \theta^Tx^{(i)}$이고
Logistic Regression 에서는 $h_{\theta}(x) = \sigma(\theta^Tx^{(i)})$이다.
'딥러닝기초' 카테고리의 다른 글
| Conv1D의 기본적인 input과 output (1) | 2023.01.18 |
|---|---|
| [선형대수]역행렬, 행렬식, 고유벡터 (0) | 2022.05.19 |
| [Density Estimation]GMM(Gaussian Mixture Model)과 EM 알고리즘 (0) | 2022.04.28 |
| [Density Estimation]K-Nearest Neighbors Estimation과 Classification (0) | 2022.04.27 |
| [Density Estimation]파젠창(KDE)으로 파라미터 추정 (0) | 2022.04.26 |



