Fourier Series
음성 녹음한 파일을 보면 복잡한 형태의 신호가 나온다. 그 이유는 다양한 주파수(frequency)를 가진 사인파 형태(sinusoidal)의 신호들이 섞여있기에 그러하다. 이때 의미있는 분석을 위해서는 time domain이아닌 frequency domain으로 살펴 어떠한 주파수의 신호들로 이루어져 있는지 알아내야 한다. 이때 이용할 수 있는 수학적 도구가 푸리에 변환(Fourier Transform)이다. 즉 푸리에 변환은 time domain에서 frequency domain으로 나타내어 해당 신호가 어떠한 주파수 성분들로 구성되는지 알 수 있도록 한다.
주기함수를 지수함수의 조합으로 표현할 수 있는 것이 푸리에 급수이다.
주기함수가 아닌 것을 지수 함수로 표현하는 것은 푸리에 변환이다. 이는 보통 에너지 신호인 경우에만 잘 된다.
에너지 신호가 아닌 신호에도 푸리에 변환을 적용하고 싶어서 어떠한 trick을 이용하는데 이를 라플라스 변환이라 한다.
1) 주기신호 - 푸리에 급수
2) Energy 신호 - 푸리에 변환
3) 일반적인 신호 - 라플라스 변환
푸리에 급수(Fourier Series)부터 보자. 푸리에 급수는 주기신호(periodic signal)를 sine 함수와 cosine 함수의 선형 결합 형태로 나타낼 수 있다는 이론이다. 핵심은, 어떤 복잡한 형태의 주기함수나 주기신호를 cosine과 sine의 선형 결합으로 표현하는 것이다.

진폭과 위상은 같고 주파수만 $f$ = 2, 4, 6, 8 로 다른 파형들이다.

위 4개의 파형을 sum하면 다음과 같이 주파수가 2인 주기함수가 된다. 당연히 제일 느리게 진동하는 친구에게 맞춰주어야 겠다.

가장 작은 주파수 $f_1$을 기준으로 하여 $2f_1, 3f_1, 4f_1, ...$의 파형을 합하면 가장 작은 주파수 $f_1$을 갖는 파형이 된다.
어떤 복잡한 주기를 가진 파형이 있고 이것의 주파수가 $f$라면 이 파형은 주파수 $f$의 정수배인 사인파들의 합으로 표현할 수 있다.
이때 진폭과 위상을 달리 해야 여러 파형의 표현이 가능하겠다.
$y(t) = b_1 \sin (2 \pi ft + \phi {_1}) + b_2 \sin (2 \pi 2ft + \phi {_2}) + b_3 \sin (2 \pi 3ft + \phi {_2}) +...$
위 식은 (0, 0)일 때만을 간주하게 된다. sin 함수밖에 없어서 그러하다. 그러므로 cos 함수도 불러오도록 한다.
$y(t) = a_1 \cos 2\pi ft + b_1 \sin 2 \pi ft + a_2 \cos 2 \pi 2ft + b_2 \sin 2 \pi 2ft + ...$
이렇게 되면 t = 0에서 임의의 값을 모두 가질 수 있다.
마지막으로 함수를 y축 기준으로 $a_0$만큼 이동한 채 이를 중심으로 진동하게끔 $a_0$을 더하면 최종적인 식을 도출해낼 수 있다.
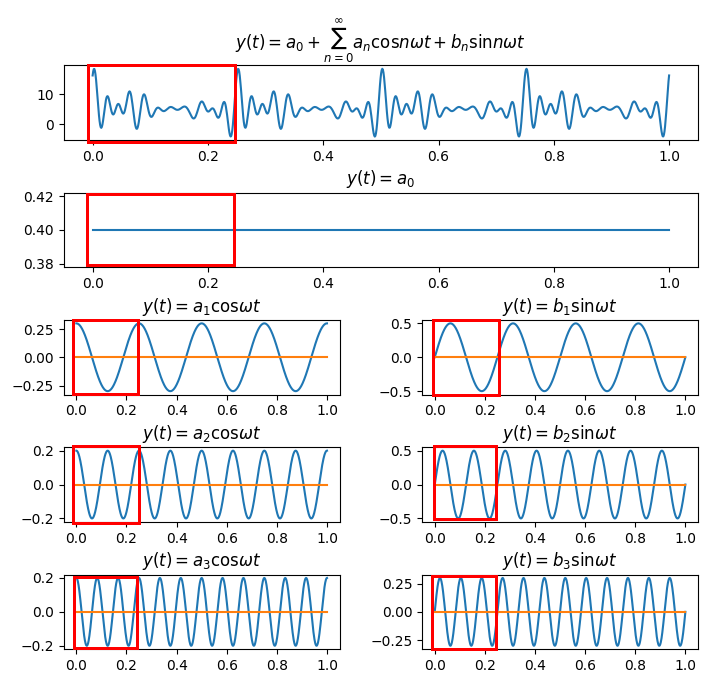
$y(t) = a_0 + \sum _{n=1}^{\infty}{a_n \cos {2\pi nft} + b_n \sin {2\pi nft} }$
$y(t) = a_0 + \sum _{n=1}^{\infty}{a_n \cos n\omega t + b_n \sin n \omega t}$
$y(t) = a_0 + \sum _{n=1}^{\infty}{a_n \cos \frac {2\pi n}{T}t + b_n \sin \frac {2\pi n}{T}t}$
복잡한 주기신호 = 주기신호1 + 주기신호2 + ... 으로 나타내는 것 뿐이다.
sin과 cos 각 항마다 계수(coefficient)인 $ a_n $ 과 $ b_n $이 곱해져있다.
또한 sin과 cos에 $ nx $ 가 input으로 들어가는데 이때 n은 주파수(frequency)를 결정한다.
$ sin(x) $는 n=1인 경우이고 $ 2\pi $까지 한번 진동한다.
$ sin(2x) $는 n=2인 경우이고 $ 2\pi $까지 두번 진동한다.
한번의 진동에 $ 2\pi $가 걸렸다.
삼각함수가 $ 2\pi $의 주기를 가지기 때문에
$ T = 2\pi / n $
그래서 $ sin(x) $의 주기는 $ 2\pi $이고,
$ sin(2x) $의 주기는 $ \pi $이다.
그렇다면 계수(coefficient)인 $ a_n $ 과 $ b_n $은?
주파수 성분들이 f에 얼마만큼 포함되어있는지 contribution을 나타낸다고 볼 수 있다. 즉 단순한 파동의 가중치.
$ b_0 = 0 $ 이기에 따로 표기하지 않았다.
$a_0$ 구하기
$a_0$은 아까 살펴본 바와 같이 y축 기준으로 $a_0$만큼 이동한 것이니 어떤 상수 값이다.
sin이나 cos이나 주기 T에 대해서 적분하게 되면 0이 나온다(2T, 3T, ...에 대해서도 마찬가지다).

주기 T에 1 cycle, 2 cycle, ...을 적분해도 상쇄되어 모두 0이 나온다.
그러므로 y절편인 $a_0$을 T만큼 곱한 면적만 살아남겠다.
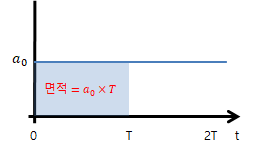
$\int _{0}^{T}{f(t)dt} = T \times a_0 + 0 + 0 + ...$
이를 정리해서 쓴다면 다음과 같다.
$a_0 = \frac {1}{T} \int _{0}^{T}{f(t)dt}$
$a_1, b_1$ 이상 계수 구하기
계수 구하기에 앞서 $m \neq n$일 때 ${1, \sin(mx), \cos(nx)}$는 $[-\pi, \pi]$의 범위에서 orthogonal하다.
이를 증명하기 위해서 사인파 함수 $w \circ v = 0$를 나타내어 본다.
벡터에서는 벡터의 내적이 0이면 직교성을 갖추는데, 함수의 직교성은 다음의 관계를 만족한다.
$\int _a^b f_1*f_2 dx = 0$
두 함수를 곱하고 주기만큼 적분한 값이 0이 나와야 한다.
(1) 모든 정수 k에 대하여 $\sin(k\pi) = 0$
(2) $\cos(m\theta) \circ \cos(n\theta) = 0$만 증명하면 되겠다.

 |
 같은 주기를 가진 경우 |
위처럼 절대값이 같은 주기를 가진 경우의 결과는 0이 아닌 $\pi$가 나온다.
이 직교성을 가지고 푸리에 계수를 구할 수 있다.
$\cos(mx)$를 곱해서 적분해보자.

$\sin(mx)$를 곱해서 적분해보자.
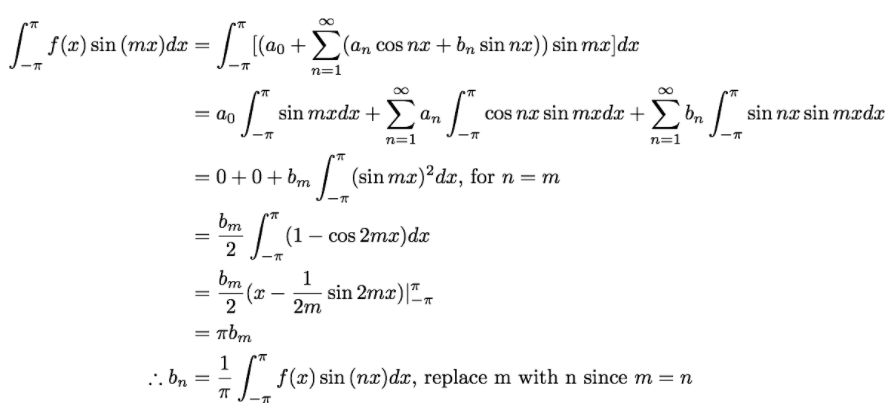
$\int _{0}^{T}{\sin(nwx)\cos(mwx)dx} = 0$
$\int _{0}^{T}{\cos(nwx)\cos(mwx)dx} = 0 (n \neq m)$
$\int _{0}^{T}{\sin(nwx)\sin(mwx)dx} = 0 (n \neq m)$
$\pi(n = m)$
위를 정리하면 계수 $a_0, a_n, b_n$를 다음을 통해 구할 수 있다.
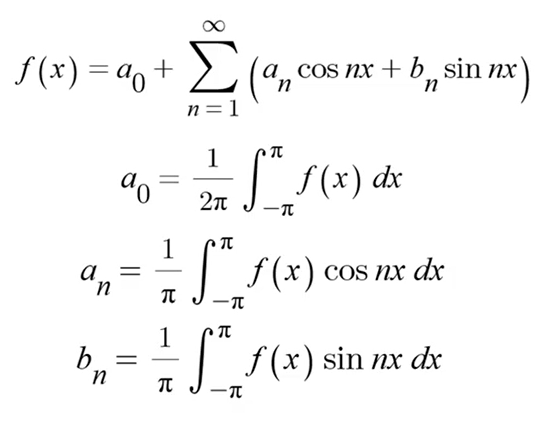
주기가 $2\pi$가 아닌 일반화된 T일 때


이때 $f(x)$가 기함수일 때 우함수인 cos 함수는 존재할 필요가 없다. $a_n = 0$
마찬가지로 $f(x)$가 우함수일 때 기함수인 sin 함수가 존재할 필요가 없다. $b_n = 0$
오일러 공식을 통해서 지수함수의 형태로 바꿔보자.
사인파 함수의 합으로 표현된 푸리에 급수를 복소지수로 표현한다.

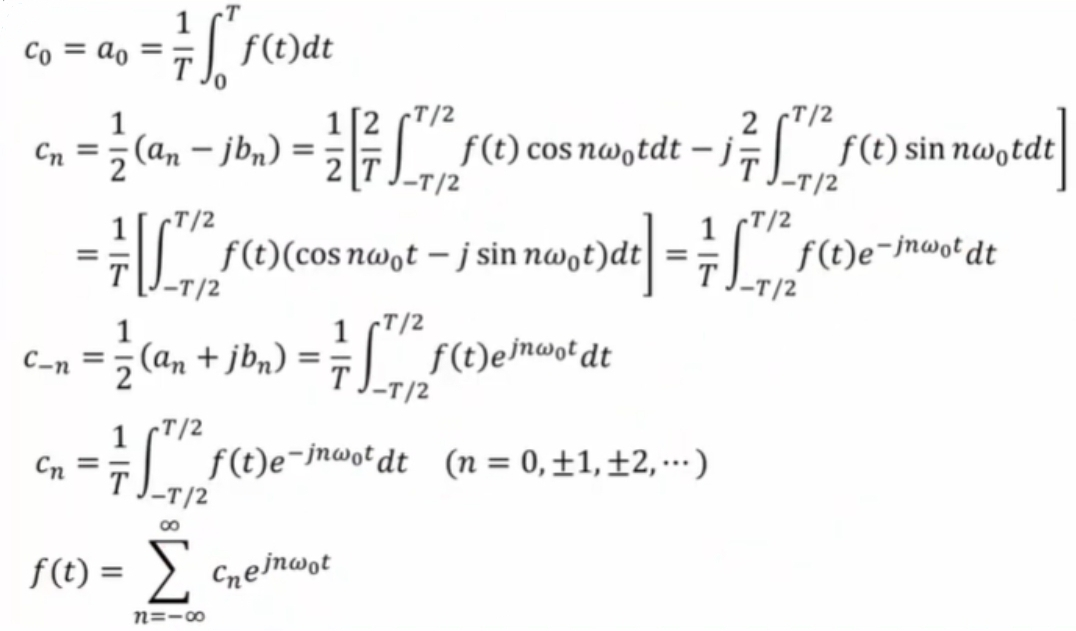
주기함수의 가장 낮은 주파수를 기준으로 정수배에 해당하는 값들만 아래와 같은 스펙트럼을 가진다.

최종적으로 지수함수로의 표현을 하면 다음과 같아진다! $C_n$을 구할 때는 주기 T에 대해서 구하는 것이 중요하므로,
$[0, T]$이던지 $[-\dfrac{T}{2}, \dfrac{T}{2}]$던지 상관 없다.


삼각함수 표현 vs 지수함수 표현
- 삼각함수 : 파(wave)의 기본 형태를 사인함수로 여기고,
기본 주파수의 정수배가 되는 모든 기본파의 합으로 주어진 파를 표현한 것이고, - 복소지수 : 파(wave)의 기본 형태를 복소평면에서의 원으로 여기고,
이 원의 기본 각속도의 정수배(양의 정수배 및 음의 정수배)가 되는 원들의 합으로 주어진 파를 표현한 것이다.
'신호처리기초' 카테고리의 다른 글
| Linear Time-Invariant System(LTI system) 정의 및 간단 정리 (0) | 2022.04.01 |
|---|---|
| LTI system 들어가기 전 계단함수와 임펄스 응답 알아보기 (0) | 2022.04.01 |
| 신호에 들어가기 전 기초 다지기 (0) | 2022.03.27 |
| DFT 알아보고 python으로 구현하기 (0) | 2020.12.15 |
| python으로 정현파(sinusoid) 만들기 (0) | 2020.12.14 |



