DFT가 나오기까지
부제) 우리 컴퓨터는 continuous 못해요! 왜 애 기를 죽이고 그래!
Fourier Transform에서 time domain에서 연속 주기 함수이니 frequency 축으로 바꿀 때는 그 한 주기에 대해서만 계산하면 된다.
반대로 frequency 축은 이산 비주기함수이니 $(-\infty, \infty)$에 대하여 계산하여 time domain으로 바꿨다.
Continuous time에 대해서 CTFT는 사람 손으로나 가능하지, 컴퓨터의 영역에서는 불가능하다.
컴퓨터가 연속을 다룰 수 없기에 그렇다.

그렇다면 컴퓨터가 다룰 수 있도록 이산신호로 바꾸어보자
Time 영역에서 Discrete한 파형을 Fourier Transform을 하면(DTFT) Frequency 영역에서 주기신호가 된다.

또 문제가 발생하였다.
비주기 신호를 DTFT하니 주파수 영역에서 continuous 그래프가 나와버린다^^
주기함수 $\leftrightharpoons $ Discrete 함수
비주기함수 $\leftrightharpoons $ Continuous 함수
Fourier Series에서 Time domain(주기, 연속)에서 Frequency domain(이산, 비주기) 넘어갈 때 생각해봐. vice versa
그래서 다시 주파수 영역에서 샘플링을 하여 이산적으로 만들어보고자 한다.
일련의 과정을 다시 정리해보자.
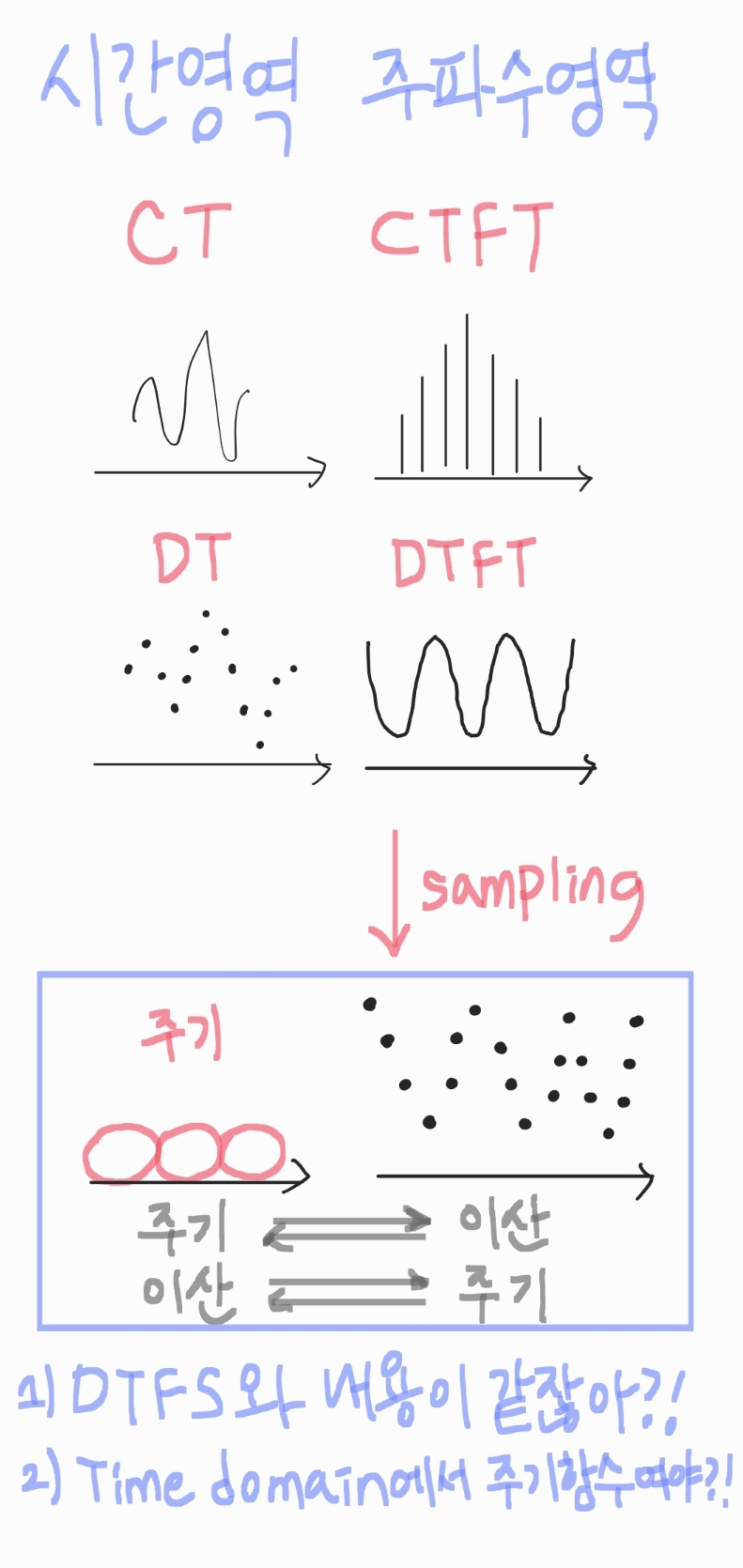
주파수 영역에서 샘플링을 하면 이산적이고 주기인 함수이고
이를 Time domain으로 바꾼다 하면 주기적이며 이산적인 함수가 되겠다.
> ... 이거 DTFS와 같은 것 아닌가?
그렇다 DTFS와 DFT는 내용적으로 같다.
그럼 무엇이 다른가?
DTFS는 주기함수를 넣었다. 그러나 DFT는 비주기함수를 커버하고자 한다.
커버하는 방법은 바로 시간이 유한한(Time Limited) 비주기함수를 주기함수인양 다루는 것이다!!!
(만약 무한한 비주기신호인 노답 끝판왕은 어쩌냐?! 이는 STFT를 통해 토막토막 잘라 각기 FT를 한다....)
아래처럼 원래 [a, b]까지의 유한한 함수인데 이것이 마치 주기함수처럼 뻔뻔하게 나가는 것이다.
주기함수 일 때는 한 주기에 대해서 계산을 하니 말이다.

한 주기에 대해서만 푸리에를 진행한다.
DFT is,
$$X[k] = \sum_\limits{n=0}^{N-1}x[n]exp\left(-j\frac{2\pi k}{N}n\right)$$
$$x[n] = \frac{1}{N}\sum_\limits{k=0}^{N-1}X[k] exp\left(j\frac{2\pi k}{N}n\right)$$
- $x_{n}$ : input signal
- $n$ : Discrete time index
- $k$ : discrete frequency index
- $X_{k}$ : k번째 frequeny에 대한 Spectrum의 값
전체 신호의 길이가 N인 이산 신호 $x[n]$에 대하여,
각주파수를 N개로 쪼갠 후 k번째 주파수에 해당하는 변환 값을 찾아내는 것이 DFT이다.
무슨 말인지 하나씩 살펴보자.
위 식을 보면 time domain에서도, frequency domain에서도 N개의 샘플을 갖는 식이다.
그렇다면 time domain에서의 신호 x[n]과 이산 주파수 성분 X[k]에 대하여 각각
$$\begin{bmatrix}x[0]\\ x[1] \\ \vdots \\ x[n] \\ \vdots \\ x[N-1]\end{bmatrix}\begin{bmatrix}X[0]\\ X[1] \\ \vdots \\ X[k] \\ \vdots \\ X[N-1]\end{bmatrix}$$
로 벡터처럼 생각할 수 있겠다.
$k = 0, 1, ... , N-1$일 때의 $X[k]$ 값을 계산해보자.
$$X[0] = x[0]\exp\left(-j\frac{2\pi 0}{N}0\right) + x[1]\exp\left(-j\frac{2\pi 0}{N}1\right)+\cdots +x[N-1]\exp\left(-j\frac{2\pi 0}{N}(N-1)\right)$$
$$X[1] = x[0]\exp(\left(-j\frac{2\pi 1}{N}0\right)+x[1]\exp(\left(-j\frac{2\pi 1}{N}1\right)+x[N-1]\exp(\left(-j\frac{2\pi 1}{N}(N-1)\right)$$
표기의 단순화를 위해서
$$w = \exp\left(-j\frac{2\pi}{N}\right)$$
이라고 한다면 i번째 주파수 성분 X[i]에 대해서
$$X[i] = x[0]w^0 + x[1]w^{i\times1}+\cdots+x[j]w^{i\times j}+\cdots +x[n-1]w^{i\times(n-1)}$$

이러한 관계로 표현할 수 있겠다.
DTFT와 DFT의 관계는
0에서 N-1까지 값을 가지는 $x[n]$을 DTFT한 후, 주파수 도메인에서 $\frac{2\pi}{N}$의 간격으로 점을 뽑아낸게 DTF라고 하였다.
$$X(k) = X(e^{j\omega})|_{\omega = \frac{2\pi}{N}k}$$
즉 주기 $2\pi$에 있어 그 안에서 N개의 점을 뽑았다.
복소 평면에서 보면 원래 $e^{i\theta} = \cos \theta + i \sin \theta$에서 $\theta$에 따라서 원 내에서 가리키는 방향이 달라졌다. 이 $\theta = \frac{2\pi}{N}$이 되었을 뿐이다.
아래는 N=8인 경우, 즉 한바퀴인 $2\pi$ 안에서 8등분하여 점을 찍은 것이다.
 |
 |
그 $\omega$가 가리키는 phase를 표시하면 다음과 같다.

phase를 cosine과 sine 함수에 대해서 생각하면 아래처럼 생각할 수 있다.
푸리에 행렬의 각 행은 주파수 0부터 fundamental frequency의 배수만큼 cosine 함수를 표현하고 있다.
 |
 |
즉 DFT 계산시 사용하는 푸리에행렬은 fundamental frequency의 배수로 구성된 cosine, sine함수들이며 이 complex number을 원래의 시간 신호와 하나하나 내적되어 결과를 얻어주는 것이다.
내적은 곧 유사도를 뜻하기도 하기에 특정 주파수에 대해서 각 샘플과 푸리에 행렬의 요소와 얼마나 닮았는지를 나타낸다 할 수 있다.

결국 DFT를 함으로써,
이산적 time domain 신호 각각으로부터 주파수 K를 얼마나 포함하는지를 알 수 있는 듯하다.
Python으로 DFT 구현해보기
import numpy as np
import matplotlib.pyplot as plt
#input
N=64
k0=7#freq
x=np.exp(1j*2*np.pi*k0/N*np.arange(N))
#output
X=np.array([])
for k in range(N):#0~N-1
#k주파수에 해당하는 샘플링된 모든 신호 더하기
s=np.exp(1j*k*2*np.pi/N*np.arange(N))
#-j라서 conjugate붙었다!
X=np.append(X, sum(x*np.conjugate(s)))
plt.plot(abs(X))
plt.show()
실행화면

'신호처리기초' 카테고리의 다른 글
| Linear Time-Invariant System(LTI system) 정의 및 간단 정리 (0) | 2022.04.01 |
|---|---|
| LTI system 들어가기 전 계단함수와 임펄스 응답 알아보기 (0) | 2022.04.01 |
| 신호에 들어가기 전 기초 다지기 (0) | 2022.03.27 |
| 푸리에급수, 어떤 의미를 지니는가 (1) | 2022.03.21 |
| python으로 정현파(sinusoid) 만들기 (0) | 2020.12.14 |



