Time Invariant

$x(t) \rightarrow y(t)$일 때 time shift된 input $x(t-t_0) $이 들어간 결과로 똑같이 shift된 $y(t-t_0)$이 나온다.
Stability에서 실험적으로 시스템이 안정한 지 알 수 없다고 이야기 하였다.
세상에 모든 유한한 입력을 가지고 test 할 수 없기 때문이다.
Time Invariant한 지에 대해서도 마찬가지이다.
모든 $t_0$에 대해서 만족하는지 다 따질 수....? 어림도 없다.
그러므로 수학적으로 보아야 한다.
$x_1(t) \rightarrow y_1(t)$
$x_2(t) \rightarrow y_2(t)$
$x_2(t) = x_1(t-t_0) \rightarrow y_2(t) = y_1(t-t_0)$인가?




Linearity
If $x_1\rightarrow y_1$ and $x_2 \rightarrow y_2$, then
1) $x_1 + x_2 \rightarrow y_1 + y_2$ (Additivity property)
2) $ax_1 \rightarrow ay_1$ (Homogenity or Scaling property)
$bx_2 \rightarrow by_2$
1)과 2)를 한번에 표현하면
$ax_1 + bx_2 \rightarrow ay_1 + by_2$
시스템이 Linear한가?에 대해서
input으로 0을 넣으면 0이 나와야 한다. (필요조건)
0이 안나오면 무조건 선형이 아니다. 0이 나오면 Linear 시스템일 '가능성'이 있는 것이다.
참고로 유한차원 LTI 시스템의 입출력은 항상 이같은 미분방정식을 만족한다.

LTI System
이전에 말했듯, 임의의 신호를 impulse 혹은 지수함수의 조합으로 나타낼 수 있다.
지금은 impulse들의 조합으로 나타날 때 어떤 특징이 있는지에 대해 이야기할 것이고
나중에 지수함수로의 조합을 통해 각기 푸리에 급수, 푸리에 변환, 라플라스 변환을 이야기할 수 있다.
시스템이 LTI 이라면 푸리에급수, 푸리에 변환, 라플라스변환이 강력해진다.
우선 시스템이 LTI 시스템일 때,
1) 신호를 impulse들의 조합으로 나타내기
2) impulse response를 알면 선형성과 시불변성을 결합하여 출력을 입력 * impulse response로 표현
그래서 impulse response만 알면 임의의 입력 signal에 대한 출력을 알 수 있다.
Impulse response가 system에 관해서 어떤 입력이 들어갈 때 어떤 출력인지 모든 것을 알고 있는 것이다.

Impulse response를 알면 그 시스템을 아는 것이다!!!
(시스템을 안다는 것은 출력을 계산할 수 있다는 의미이다)
고로 system에 관한 이야기를 impulse response에 관한 이야기로 환원할 수 있다.
1) 신호를 impulse들의 조합으로 나타내기
신호를 하나하나씩 임펄스 함수로 샘플링하는 느낌으로 신호를 표현한다.

$$x[n] = \sum_\limits{k=-\infty}^{\infty} x[k]\delta[n-k]$$
물론 x[n]에는 어떤 이산 신호가 오더라도 ok이다!
2) 자, 그래서 impulse로 이루어진 신호를 넣어보자.
우리는 시스템이 LTI를 만족한다고 보고 진행하는 것임을 기억하자!
2-1) 시스템이 Linear를 만족

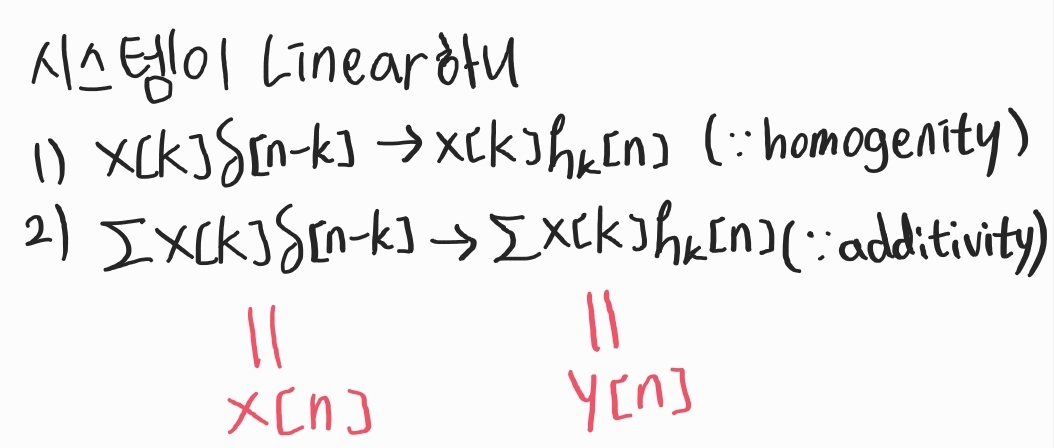
$y[n] = \sum_\limits{k=-\infty}^{\infty}x[k]h_k[n] = x[n] * \delta [n]$$ (Convolution의 정의)
2-2) 시스템이 Time Invariant를 만족

$y[n] = \sum_\limits{k=-\infty}^{\infty}x[k]h_0[n-k]$
그러므로 $h_0$ 하나만 알면 임의의 입력 x에 대한 시스템의 출력을 알 수 있게 되는 것이다!!!
(그리고 위는 Convolution $x[n] * h[n]$의 정의이다!!!)
정리하자면
$x[n] = \sum x[k]\delta[n-k] = x[n] * \delta[n]$ (Convolution) 으로 시작
$\delta[n] \rightarrow h[n] := h_0[n]$이라 할 때
$y[n] = \sum_\limits{k=-\infty}^{\infty}x[k]h[n-k]$
$=\sum_\limits{k=-\infty}^{\infty}x[n-k]h[n]$ (Convolution의 교환법칙 성립)
$=x[n] * h[n]$ (Convolution)
입력과 impulse response의 convolution으로 출력을 계산할 수 있다.
입력을 $\delta[n]$으로 나타내는 것도 convolution,
impulse response $h[n]$으로 출력을 계산하는 것도 convolution이다.
$$x[n]*\delta[n] \rightarrow x[n] * h[n]$$
'신호처리기초' 카테고리의 다른 글
| [푸리에]푸리에를 들어가기 전 지수함수와 eigenfunction (0) | 2022.06.11 |
|---|---|
| [신호와시스템]연속시간 LTI시스템과 impulse로 신호 나타내기 (0) | 2022.05.31 |
| [신호와시스템]시스템의 성질 (0) | 2022.05.26 |
| [신호와시스템]Impulse에 대해 알아보기 (0) | 2022.05.25 |
| [신호와시스템]신호의 기본개념(3) - 지수함수 (0) | 2022.05.25 |



