지수함수는 eigenfunction이다!!!!! 를 외치고 시작하겠다.
고유벡터와 고유함수
우선 eigenvector와 eigenfunction간 관계를 보자.
$$Av = \lambda v$$

행렬 A라는 선형변환(연산자)을 v에 가함으로써, 방향은 같되 크기만 달라질 때($\lambda$만큼)
이때의 v를 eigenvector 고유벡터, $\lambda$를 eigenvalue 고유치 라고 한다.
Eigenfunction
위의 개념을 그대로 갖고와서 $Av = \lambda v$의 방향에 해당하는 것이 여기서는 함수의 생김새이다. 그리고 이는 곧 eigenfunction이다.

특별히 이 eigenfunction에 해당하는 함수가 지수함수이다.

LTI 시스템일 때에는 impulse를 시스템에 넣어 impulse response인 $h(t)$를 얻는데
$h(t)$만 알면 어떠한 $x(t)$가 들어와도 convolution으로 출력을 계산할 수 있다 했다.
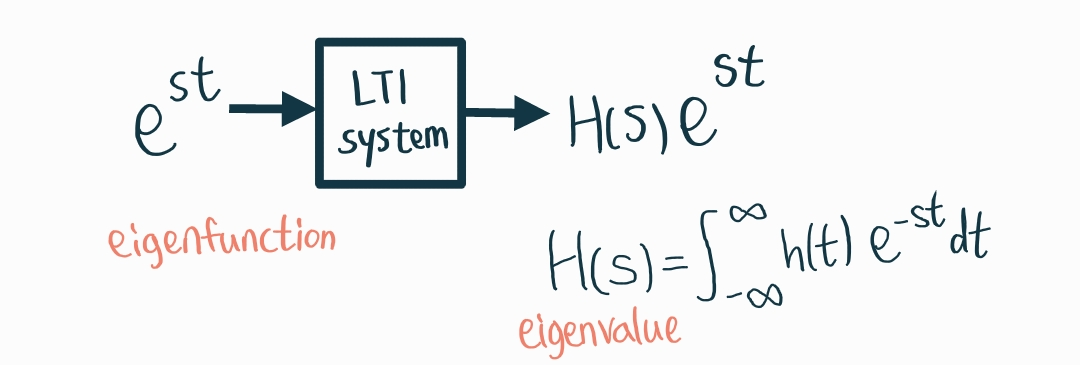
그래서 impulse response인 $h(t)$를 갖고 있다고 하고 입력으로 지수함수를 넣으며 아래대로 흘러가보자.

$$H(s) = \int^{\infty}_{-\infty}h(\tau)e^{-s\tau}d\tau$$
위 H(s)가 $\lambda$역할을 하게 되고 곧 이 H(s)가 존재해야만(정의되어야) eigenvalue 역할을 할 수 있다.
H(s)를 frequency response라고 부르기도 한다. $s=\sigma + jw$로의 복소수일 때 주파수는 $w$이겠다. 그러한 $e^{st}$가 입력으로 들어갈 때 특정 주파수 $w$가 얼마나 더 혹은 덜 weighted되는가로 볼 수 있겠다.
지금까지는 연속시간에 대한 이야기. 이산 시간을 살펴보자.
이산에서의 eigenfunction 지수함수는 $z^n$이라고 칭한다.

그러므로 이산의 eigenvalue에 해당하는 함수는
$$H(z) = \sum_\limits{k=-\infty}^{\infty}h[k]z^{-k}$$
이산의 $z^n$과 연속의 $e^{st}$의 관계는 어떻게 되는 것일까?

다시 연속으로 돌아와서 Eigenfunction의 조합을 입력으로 넣어보자.
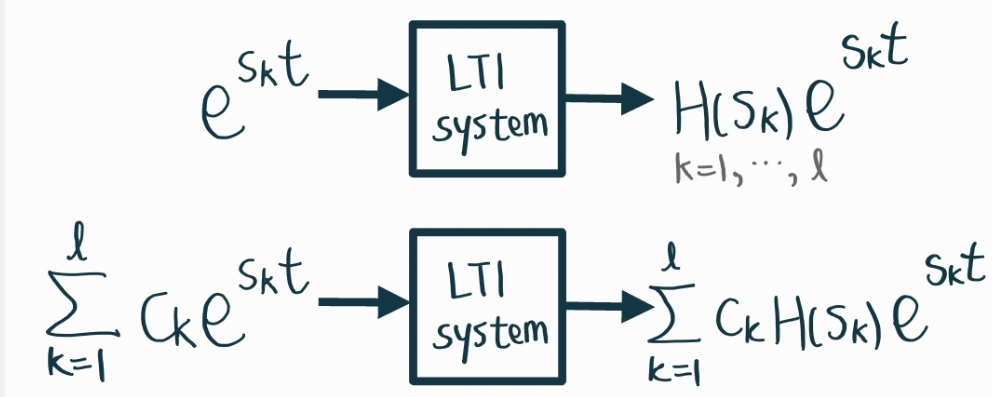
Eigenfunction의 조합이 입력으로 들어가면 선형성 덕에 eigenvalue 가지고 출력을 구할 수 있다.
신호를 지수함수의 조합으로 나타낼 때 일반적으로 의미있지만 특히 Linearity를 만족하는 LTI일 때 더더욱 그러하다.
푸리에를 들어가기 전...
우리는 주기신호를 주기 T를 공유하는 지수함수의 조합으로 표현할 수 있다.
$$x(t) = \sum_\limits{k=-\infty}^{\infty}a_k\phi_k(t)$$
where $\phi _k(t) = e^{jkw_0t} = e^{jk\frac{2\pi}{T}t}$ ( k = ..., -1, 0, 1, ... )
아래에서는 신호 y1의 주기가 제일 긺으로 기본 주기가 되고
해당 주기를 공유하는 신호의 조합 y1 + y2 + y3가 신호 y가 된다.
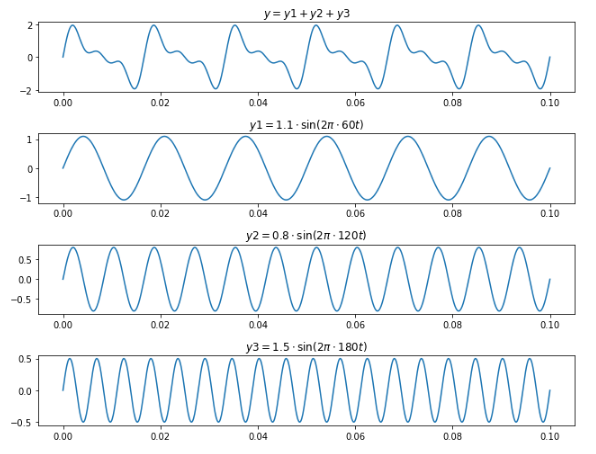
그렇다면 주기 T를 공유하지 않는 비주기함수에 대해서는 어떻게 하는가?
어떤 특성을 가진 신호 $x(t)$을 가지고 하느냐에 따라 s가 달라지고,
- $s = jkw_0$ → 푸리에 급수
x(t) = x(t+T) 주기 T를 갖는 신호를 eigenfunction 즉 지수함수의 조합으로 - $s=jw$ → 푸리에 변환
비주기신호를 eigenfunction의 조합으로(그러나 에너지 신호인 경우만 잘됨) - $s = \sigma + jw$ → 라플라스변환
에너지 외 비주기 신호에 대해서도 가능케하려 신호에 어떠한 조작후 푸리에 변환
전반적으로 정리하자면 우리는 신호를 1) impulse로 나타내는 것과 2) 지수함수로 나타내는 것이 가능하다고 했다. 1)은 impulse 함수와 LTI 시스템을 함께 다루며 언급하였고 앞으로는 지수함수로 신호를 나타내는 것 및 그에 따른 장점을 살펴볼 것이다.

$\phi _k(t) = e^{jkw_0t} = e^{jk\frac{2\pi}{T}t}$ k = ..., -1, 0, 1, ...
주기를 공유하는 정현파들의 조합으로 표시할 수 있다면 k가 무한히 곱해질 수 있으니 무한급수 형태이겠다.
$$x(t) = \sum_\limits{k=-\infty}^{\infty}a_k\phi_k(t)$$
이와 달리, 이산 주기신호에서는 "가장 빨리 변하는 신호의 주파수" 라는 것이 존재한다($\pi$). 이는 주기가 N = 2일 때 위, 아래, 위, 아래를 나타낼 때이다. 그러므로 연속에서와는 다르게 주기를 공유하는 정현파의 개수가 주기 수 N개이다.
그러므로 이산시간 푸리에급수(DTFS)는 "주기 수"만큼의 함수의 조합으로 표현한다. 그래서 이산시간 푸리에 급수는 항상 전개 가능하다. (극한이 없으므로)
반대로 연속시간 푸리에 급수는 무한대의 개념이 존재하여 극한이 있다. 그러므로 수학적으로 전개를 못하는 상황이 올 수 도 있다.
'신호처리기초' 카테고리의 다른 글
| [푸리에급수]연속시간 푸리에 급수의 성질 (0) | 2022.07.06 |
|---|---|
| [푸리에급수]푸리에 급수의 계수 구하기 (0) | 2022.06.28 |
| [신호와시스템]연속시간 LTI시스템과 impulse로 신호 나타내기 (0) | 2022.05.31 |
| [신호와시스템]시스템의 성질(2)과 LTI시스템 (0) | 2022.05.27 |
| [신호와시스템]시스템의 성질 (0) | 2022.05.26 |



