푸리에 급수의 성질 에 대해서 이야기해보자.
1. Linearity
x, y의 주기가 같다는 전제 하에 진행된다.

두 함수의 선형 조합의 푸리에 급수 계수는 두 함수 푸리에 급수 계수의 선형 조합이다.
2. Time Shifting

이때 진폭 스펙트럼은 변화가 없다.
$|b_k| = |a_k|$
생각해보면 함수를 이동시킨다 한들, 비중이 달라지지는 않겠다.
Time domain에서의 이동은 frequency domain에서 지수함수를 곱한다(Time shifting).
반대로 time domain에서 지수함수를 곱하는 것은 frequency domain에서 이동이다(Frequency shifting).
3. Time Reversal

4. Time Scaling

$\alpha$배 scaling되면 fundamental frequency가 변한다.
이때 고조파 간 비중을 나타내는 푸리에 계수 $a_k$는 변하지 않는다.
5. Multiplication

한쪽 도메인에서의 곱은 다른 도메인에서의 convolution이다.
6. Conjugation and Conjugate Symmetry

x(t)가 real이라면(≡ $x^*(t) = x(t))$, 푸리에 급수 계수는 conjugate symmetric하다($a_{-k} = a^*_k$)
x(t)가 real and even이라면, $a_k$는 real and even이다.
x(t)가 real and odd이라면, $a_k$는 순허수 and odd이다.
7. Parseval's Relation

주기 신호의 Power은 time domain과 frequency domain 모두 같다.
(이를 푸리에변환으로 확장하면 Energy는 두 도메인에서 모두 같다)
8.

미분이 곱하는 것이 되고 적분이 나누는 것이 된다.
주기 신호를 미분하면 무조건 주기신호이지만
주기신호를 적분하면 주기신호일 수도 있고 아닐 수도 있다.
주기신호인 경우는 $a_0 = 0$인 경우이다.
어떻게 보면 당연하다. 적분을 하면 적분상수가 생겨서 그 상수는 보통 따로 구해준다.
푸리에 급수가 이용된 특수한 케이스을 살펴보자.
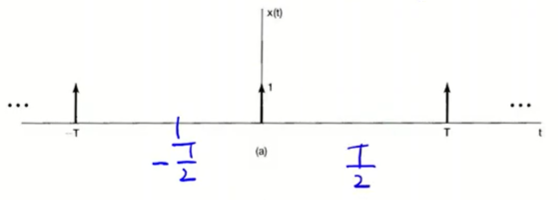
Impulse가 주기적으로 나열된 모습이다.
이를 Impulse Train이라고 부른다.
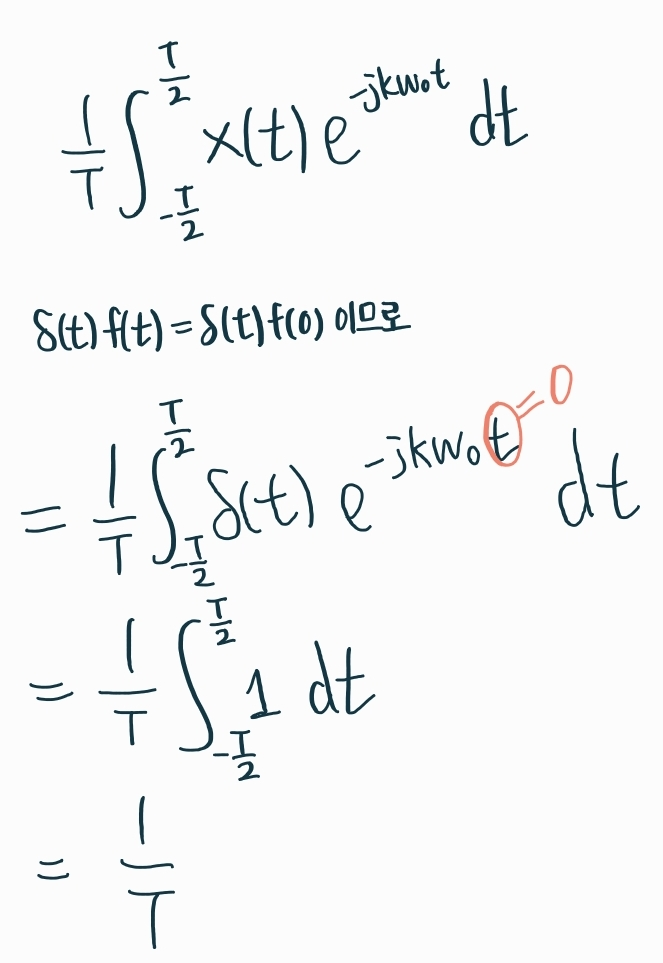
결과를 보면 k와 무관하게 $\dfrac{1}{T}$ 로, 굉장히 신기하다. 보통은 주파수가 커짐에 따라서 성분/비중이 줄어든다. 그런데 이 impulse의 경우는 주파수가 아무리 커져도 비중이 줄지 않고 일정하다.
조금 더 들어가보자.
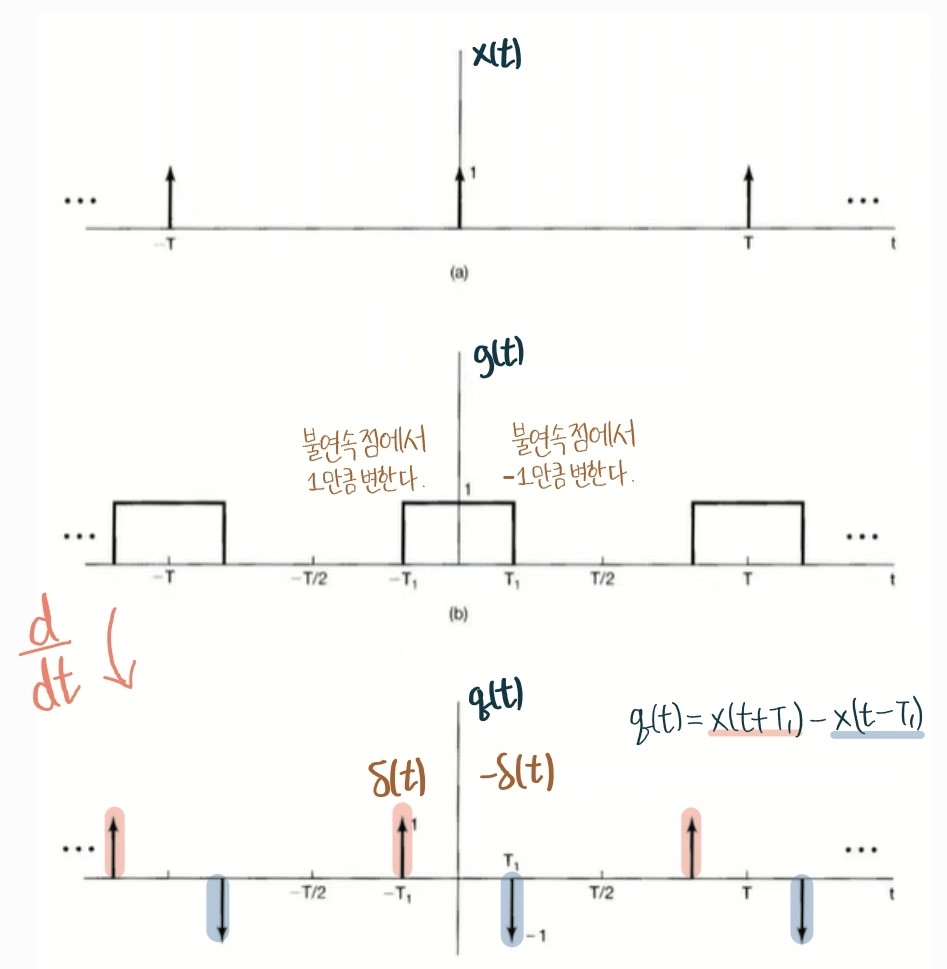
1만큼 불연속점에서 변하는 부분을 미분하면 $\delta(t)$, -1만큼 불연속점에서 변하는 부분을 미분하면 $-\delta(t)$ 로 표현한다. 이에 의거하면 $\dfrac{d}{dt}g(t) = q(t)$의 관계가 되겠다.
$g(t)$의 직류성분은 $q(t)$로 구할 수 없고 별도로 구해야 한다. 적분상수 c가 붙는 부분은 당연히 따로 구해야 맞겠다.
이와 반대로 $q(t)$의 직류 성분은 $g(t)$로 구할 수 있다. g의 미분만 하면 되기 때문이다.
$x(t), g(t), q(t)$의 관계를 통해서 푸리에 급수 계수를 구해보자.
위의 성질을 적당히 짬뽕시키면 푸리에 급수 계수를 구할 수 있다.

정확히는 푸리에급수의 성질을 이용하여 이동, 선형, 미분을 이용했다.
그럼 이제 다음 시간에는 이산 시간 푸리에 급수 (DTFS)를 본 뒤 LTI 시스템과의 관계를 살피자!
'신호처리기초' 카테고리의 다른 글
| [푸리에급수]푸리에급수와 LTI 시스템 (0) | 2022.07.14 |
|---|---|
| [푸리에급수]DTFS 유도하기 (0) | 2022.07.11 |
| [푸리에급수]푸리에 급수의 계수 구하기 (0) | 2022.06.28 |
| [푸리에]푸리에를 들어가기 전 지수함수와 eigenfunction (0) | 2022.06.11 |
| [신호와시스템]연속시간 LTI시스템과 impulse로 신호 나타내기 (0) | 2022.05.31 |



