지수함수는 Eigenfunction이다
이전에 Eigenvalue $H(s)$와 Eigenfunction $e^{st}$과 관련한 이야기를 했었다.

이때 선형성을 만족한다는 점에서 아래의 선형결합 형태 역시 구할 수 있다고 이야기했다.
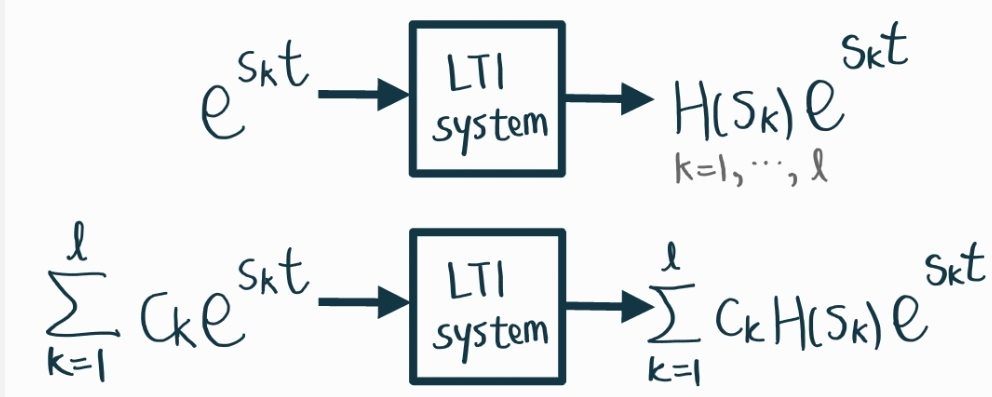
여기서 이야기를 더 진행시켜보자.
저 입력 신호 $\sum$ 쪽을 푸리에 급수 형태로 나타내는 것도 가능해보인다.
그럼 출력을 연속 y(t), 이산 y[n] 로 구할 수 있다.

위의 무한 개수의 정현파의 조합으로 이루어진 $x(t)$와 $x[n]$에서 정현파 하나를 찝어내본다고 하자.
연속시간에서는 Eigenfunction을 $e^{st}$에서 $s=jw$한 $e^{jwt}$을,
이산시간에서는 Eigenfunction을 $z^n$에서 $z=e^{jw}$한 $e^{jwn}$을 LTI 시스템에 넣어보면 다음과 같다.

우리는 보통 복소수를 크기와 위상을 가지고 표현할 수 있다.
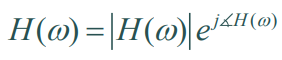
이런 점에서 출력 $y(t)$를 바라보면 $H(w)$만큼 Eigenfunction이 변화했다고 볼 뿐 아니라,
동일한 주파수의 정현파가 나오되, Eigenvalue의 진폭과 위상만큼 변화가 있다고 볼 수 있겠다.

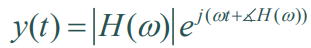
$x(t)$를 푸리에 급수로 표현한 것에 적용하면
$$x(t) = \sum_{k=-\infty}^{\infty}c_ke^{jkw_0t} \to y(t) = \sum_{k=-\infty}^{\infty} d_ke^{jkw_ot}$$
이때 $d_k = H(kw_0)c_k$ 이고 이에 대한 진폭과 위상을 구하면 다음과 같다. 그래서 출력에 대해서 크기는 Eigenvalue의 크기만큼 변화되었고 위상은 Eigenvalue의 위상만큼 달라졌다고 볼 수 있다.
$$|d_k| = |H(kw_0)|c_k|, \measuredangle d_k = \measuredangle H(kw_0) + \measuredangle c_k$$
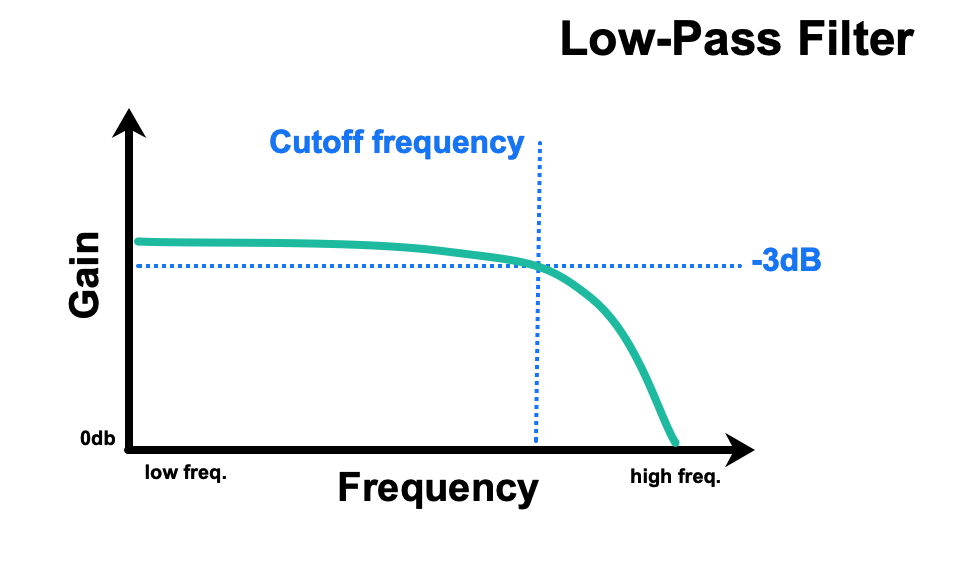
시스템을 Filter이라는 관점으로 바라볼 수 있다. 음악을 들을 때 베이스 소리가 중요해서 저주파 영역을 증폭하는 것도 Filter을 통과한 것이다.
1) lowpass filter
2) highpass filter
3) bandpass filter

'신호처리기초' 카테고리의 다른 글
| 나이퀴스트 Sampling이 나오기까지 (4) | 2022.09.29 |
|---|---|
| [라플라스변환]푸리에변환과 라플라스 변환 (0) | 2022.07.20 |
| [푸리에급수]DTFS 유도하기 (0) | 2022.07.11 |
| [푸리에급수]연속시간 푸리에 급수의 성질 (0) | 2022.07.06 |
| [푸리에급수]푸리에 급수의 계수 구하기 (0) | 2022.06.28 |



