[라플라스변환]푸리에변환과 라플라스 변환

신호를 지수함수의 조합으로 나타내는 것을 주기신호에 대해서(푸리에 급수), 비주기신호 중 유한한 신호에 대해서(푸리에 변환) 다루었다. 이제는 신호가 발산하는 경우에 대해서 어떻게 다루어야 할 지 살펴보자.

 

지수함수는 eigenvalue H(s)가 존재한다면 eigenfunction이 될 수 있다고 했다.

 

$$H(s) = \int^{\infty}_{-\infty}h(t)e^{-st}dt$$

 

(여기서는 $H(s)$가 eigenvalue로서가 아닌, $h(t)$의 라플라스변환으로 해석될 예정이다.)

 

 

$H(s)$가 존재할 조건으로 Stability가 있다. 시스템이 안정하면 $\int^{\infty}_{-\infty}|h(t)|dt < \infty$를 만족하여 $H(jw)$가 존재한다. $H(jw)$가 존재하는 안정한 시스템에 Energy 신호를 넣으면 푸리에 변환이 존재하고 Convolution이 다른 도메인으로 넘어가면서 곱하기가 된다.

$$y(t) = h(t)*x(t) \rightarrow Y(jw) = H(jw)X(jw)$$

 

이제는! 불안정한 시스템일지언정 $H(s)$가 존재할 수 있도록 하자.

즉, 비록 $s = \sigma + jw$에서 $\sigma = 0$ 경우의 $s=jw$인 $H(jw)$가 존재하지 않더라도, 0이 아닌 다른 실수 $\sigma$를 넣어봤더니 그 복소수 $s=\sigma + jw$에 대해서 H(s)가 존재할 수 있는 것이다.

 

$x(t)$의 푸리에변환

$$X(jw)=F\left\{ x(t)\right\} = \int_{-\infty}^{\infty}x(t)e^{-jwt}dt$$

 

$x(t)$의 라플라스변환(s는 복소수)

$$X(s)=L\left\{ x(t)\right\}=\int_{-\infty}^{\infty}x(t)e^{-st}dt$$

 

이때 라플라스변환은 모든 s에 대해서 X(s)가 존재할 필요가 없다. 특정한 s에 대해서만 존재하면 X(s)가 존재한다고 할 수 있다. 그러니까 특정한 $\sigma$에 대해서 X(s)가 존재하면 된다.

 

 

푸리에변환과 라플라스변환의 관계를 따져보면,

라플라스변환은 모든 $\sigma$에 대해서 존재성을 살피는 것이고, 푸리에변환은 $\sigma = 0$의 경우에서만 존재성을 살피는 것이다.

푸리에변환이 존재하면 항상 라플라스변환이 존재한다. 푸리에변환이 존재한다는 의미는 라플라스변환의 입장에서 $s = \sigma + jw$에서 $\sigma = 0$일 때인 특정 s에서 존재하는 것이기 때문이다. 그러나 그 역은 성립하지 않는다. 역이 성립하기 위해서는 $\sigma = 0$일 때 $X(s)|_{s = jw} = X(jw)$이 가능해야 한다.

 

 

그래서 라플라스변환이 뭔데!!

 

$s$에서 실수 $\sigma$를 더한다고 했는데 실제로 $s = \sigma + jw$를 대입해보고 그 의미를 파악해보자.

 

$\int_{-\infty}^{\infty}x(t)e^{-(\sigma+jw)t}dt$

$= \int_{-\infty}^{\infty}[x(t)e^{-\sigma t}]e^{-jwt}dt$

$=F\left\{ {x(t)e^{-\sigma t}}\right\}$

 

x(t)의 라플라스변환은 곧 x(t)에 $e^{\sigma t}$를 곱한 것의 푸리에변환이다.

공돌이의 수학노트

유한한 에너지함수는 푸리에 변환 가능하므로 기존에 발산하는 함수 $x(t)$에 지수함수를 곱해서 0으로 수렴하게 만들고(면적을 유한하게 하여 에너지신호로) 푸리에 변환을 진행한다.

 

정리해보자면,

라플라스변환이 무엇인가? 푸리에변환을 못하는 신호를 조작하여 푸리에변환이 가능토록 하는 것.

어떤 조작을 하는가? 발산하는 신호에 지수함수를 곱함으로써 유한한 에너지 신호로 바꾼다.

어떤 지수함수를 곱하나? $e^{-\sigma t}$이고 $\sigma$는 s의 실수부분 $Re\left\{s\right\}$이다.

그럼 모든 s에 상관없는가? 아니다. 주어지는 $x(t)$를 유한하게 만드는 특정 범위의 복소수 s이다.

 

 

푸리에변환에서의 수렴(존재)과 발산(존재 x)의 key는 a 즉 신호 그 자체이다.

<수렴과 존재성을 같은 의미로 보자>

그러나 Laplace Transform으로 넘어와서는 그 수렴 및 발산의 책임을 s에게, 정확히는 실수 $\sigma$에게 떠넘기는 느낌이다. 

그렇게 되니 푸리에변환에서는 신호가 어떠해야하느냐가 핵심이라면,

Laplace Transform에서는 s가 (신호와 관련하여) 어떠해야하느냐가 중요해지는 것이다.

 

 

 

전격 비교해보자.

 

푸리에변환

$x(t) = e^{-at}u(t)$ 인 상황을 보자.

 

 

그림으로 봐도 a가 양수일 때 함수가 유한한 면적을 갖게 되겠다.

 

$X(w) = \int^{\infty}_{-\infty} x(t)e^{-jwt}dt$

 

$= \int^{\infty}_{0} e^{-at}e^{-jwt}dt$

 

$= \dfrac{1}{a+jw}[e^{-(a+jw)t}]^{\infty}_0$

 

여기서 수렴하면서 푸리에 변환이 존재하기 위해서는 $a+jw$가 양수여야 한다.

그래야 X(w)가 발산하지 않고 값을 갖는다!

 

 

푸리에 변환 존재 조건 : $a+jw>0$

 

푸리에변환에서의 존재성의 key는 a, 즉 신호 그 자체이다.

 

라플라스 변환

 

$X(s) = \int^{\infty}_{-\infty} x(t)e^{-st}dt$

 

$= \int^{\infty}_{0} e^{-at}e^{-st}dt$

 

$= \dfrac{1}{s+a}[e^{-(s+a)t}]^{\infty}_0$

 

여기서 수렴하려면 $Re${$s+a$} > 0 즉 $Re[s] > -a$ 이어야 한다.

 

그래서 라플라스변환을 이야기할 때는 s의 제약과 함께 이야기해야 한다. 

$X(s) = \dfrac{1}{s+a}$   for Re{s} > -a

 

라플라스 변환의 존재성은 s, 정확시는 s의 실수 부분에 달려있다.

 

Laplace Transform으로 넘어와서는 수렴 및 발산의 책임을 s에게, 정확히는 실수 $\sigma$에게 떠넘기는 느낌이다. 아까부터 계속 말했듯이 어떤 $\sigma$를 $jw$에 더해서 잘 되더냐를 보는 것이니 푸리에변환에서는 a가 어떠해야하느냐가 핵심이라면, Laplace Transform에서는 s가 (a와 관련하여) 어떠해야하느냐가 중요해지는 것이다.

 

그러면 이제는 모든 a에 상관없이 라플라스변환이 가능하다고 말할 수 있다. 푸리에변환에서는 수렴의 책임이 a에게(신호에) 있던 것을, 이제는 어떤 신호에도 상관없이 어떤 지수함수가 곱해지느냐(s가 어떠해야하나)로 책임이 전가된 느낌이다. 그리고 s에 걸리는 수렴 조건은 a와 관련하다. s의 실수부분이 중요함을 다시한 번 확인할 수 있다.

 

a > 0일 때

 

$Re[s] > -a$를 만족하는 s가 jw가 될 수 있다는 것이다.

jw는 항상 수렴 영역에 존재한다.

그래서 s 대신 jw를 대입 가능하다. $(\sigma = 0)$

 

 

라플라스 변환이 존재하기 위한 영역

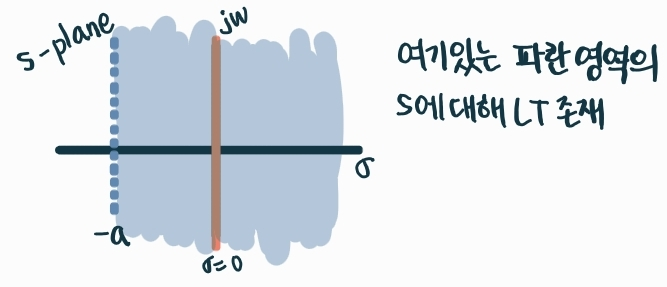
지수함수를 곱하지 않아도 에너지 신호이니 s 대신 jw 대입이 가능하다.

 

a<0일 때

라플라스 변환이 존재하기 위한 영역은 다음과 같아진다.

 

 

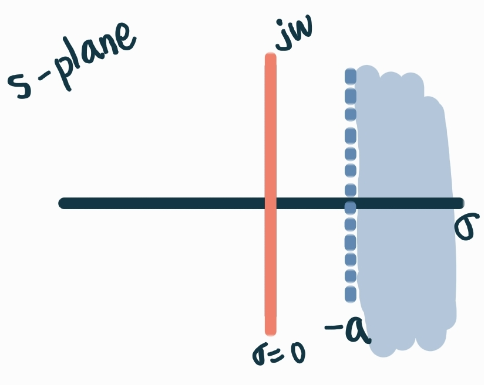이 때 s=jw는 수렴영역 밖에 있으므로 a<0일 때에는 라플라스변환은 존재하나 푸리에변환은 존재하지 않는다.

 

a=0일 때

라플라스 변환의 수렴하는 영역이 $Re[s] > 0$ : 실수부분이 0보다 큰 복소수집합이 된다.

 

 

 

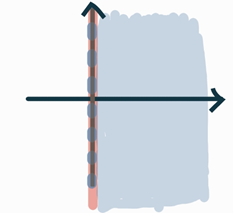이론상으로는 jw축이 수렴 영역에 포함되지 않아서 푸리에 변환이 존재하지 않는다.

 

그러나 이 계단함수에 있어서는 예외적으로 푸리에 변환이 존재한다.

 

 

$$F[u(t)] = \dfrac{1}{jw} + \pi\delta(w)$$

 

 

s의 존재 영역[수렴영역]을 Region of Convergence의 준말로 ROC라 부른다.

 

위처럼 $x(t)=e^{-at}u(-t)$를 라플라스 변환하면 똑같이 $\dfrac{1}{s+a}$이 나온다.

분명 다른 함수인데 동일한 라플라스 변환값을 갖는다는게 말이 되나..?!?

이렇게 되면 일대일 대응이 필수인 역변환도 존재하지 않을 것이다!

그럼 대체 무엇인가? 두 함수는 라플라스 변환 값은 존재하나, s의 정의역이 다르다.

 

$e^{-at}u(t)$는 $Re[s] > -a$

$-e^{-at}u(-t)$는 $Re[s] < -a$

 

이고 두 수렴 영역의 교집합은 존재하지 않는다. 그러니 엄연히 다른 함수인 것이다.

 

 

 

$x(t) = e^{-at}cos(w_0t)u(t)$의 라플라스 변환을 구해보자.

 

 

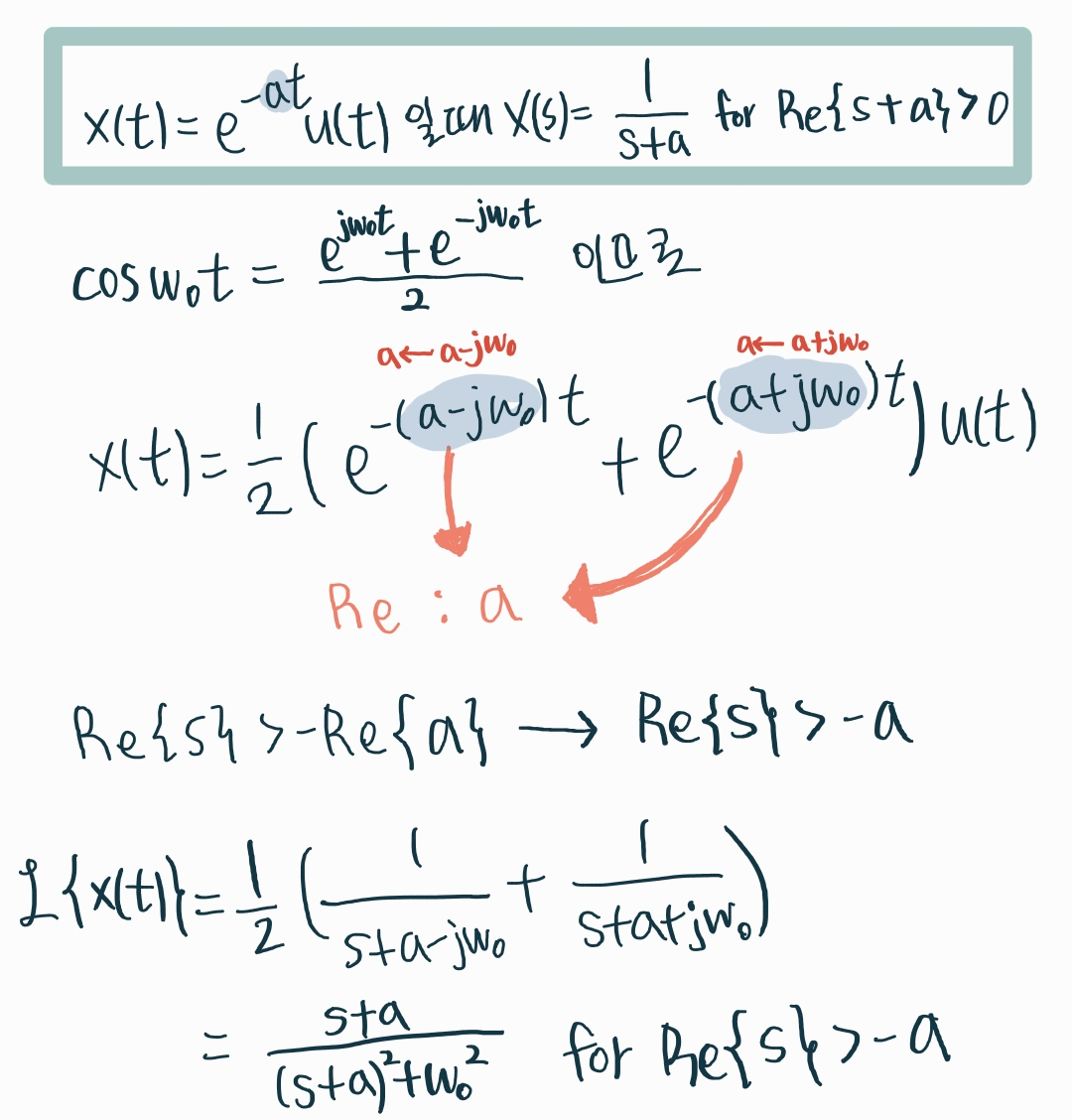
지수함수가 둘이지만 둘의 수렴 영역이 같다.

 

 

$x(t) = \delta(t)$일 때

수렴 영역이 전체 복소 평면인 예외적인 사례이다.

 

$X(s) = \int^{\infty}_\infty\delta(t)e^{-st}dt = 1 $ for all s