DTFS
연속시간을 봤으니 이제는 푸리에급수 이산시간 버전에 대해서 알아보자.
지수함수와 주기를 공유하는 정현파에 대해서 말할 때에 연속은 주기신호를 이루는 정현파가 무한히 많은 데에 반해,
이산은 주기신호를 이루는 정현파가 딱 주기 개수 만큼 있다고 이야기했다.
직관적으로 생각해보자.
이산에서는 최대주파수라는 개념이 존재했고 이는 곧 매 time 마다 바뀔 때를 말한다.

$x[n] = x[n+2]$이고 이때의 주기는 2, 주파수는 $\pi$이다.
곧 이산에서의 최대주파수는 $\pi$이고, $2\pi$씩 같은 개형이 반복된다.
그럼 위와 같은 신호는 N=2이므로 두 개의 정현파로 이루어진 것이겠다.

이때 하나는 k=0으로 상수항(높이)이 되고
k=1인 경우가 그래프의 개형을 결정짓게 되겠다.

연속시간과의 가장 큰 차이점은 무한의 개념에서 유한으로 왔다는 것이다.
얼마나 유한한가? 주기 수인 N개다.
우선 $\phi_k$는 모든 k에서 시간 n에 대하여 주기가 N인 정현파이다.
$$\phi_k[n]=\phi_k[n+N]$$
이때 지수함수가 $2\pi$마다 반복되므로 시간 n에 대하여 주기신호이지만서도,
k차 고조파 성분에 대해서 생각해도 N이 주기인 주기신호이다.
원이 계속 뺑글뺑글 돌기 때문이다.
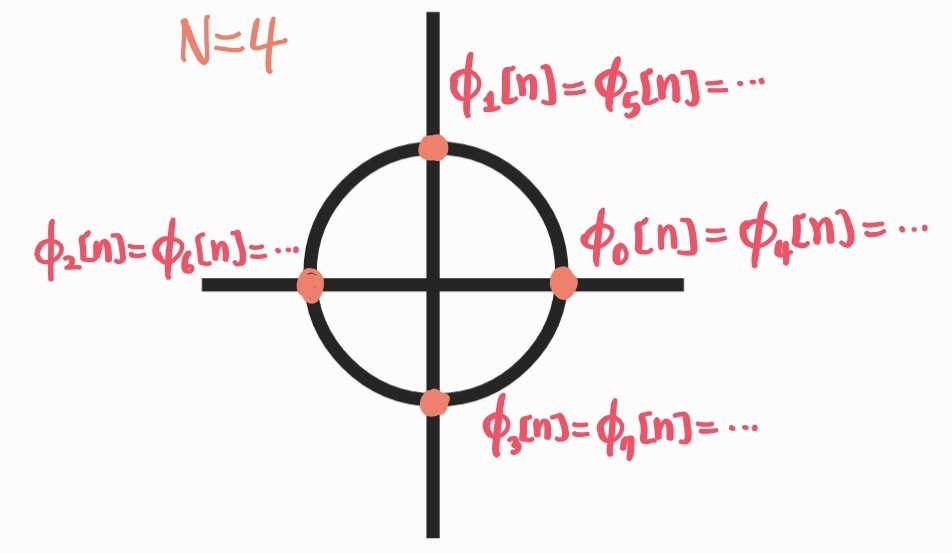
주기 N=4일 때 $\phi_0[n]=\phi_4[n]=...=1$
주파수가 N차 고조파 성분 = 직류성분
$$\phi_k[n] = \phi_{k+N}[n]$$
그러니 이산신호의 주기가 N이라면 n domain에서도, $\Omega$ domain에서도 모두 N이 주기이다.
이산신호를 지수함수로 나타내기
그렇게 N개의 지수함수의 조합으로 이산신호를 표현한다.
$$x[n] = x[n+N] = a_0\phi_0[n]+a_1\phi_1[n]+ ...+a_{N-1}\phi_{N-1}[n]$$
자연스레 $a_k = a_{k+N}$도 만족하게 된다. 성분의 함유량도 같을 수 밖에 없겠다.

연속에서와 마찬가지로 직교성을 통해서 $a_k$를 구할 수 있다.
$a_k$ 계수를 구할 때에는 $x[n]$을 이용하니 n에 관하여 summation이,
$x[n]$을 구할 때에는 k에 관한 summation을 진행한다는 부분을 놓치지 말자.
또한 $x[n]$과 $a_k$의 관계
$x[n] = a_0\phi_0[n]+a_1\phi_1[n]+ ...+a_{N-1}\phi_{N-1}[n]$
이를 다음처럼 나타내는 것이 가능하다.

'신호처리기초' 카테고리의 다른 글
| [라플라스변환]푸리에변환과 라플라스 변환 (0) | 2022.07.20 |
|---|---|
| [푸리에급수]푸리에급수와 LTI 시스템 (0) | 2022.07.14 |
| [푸리에급수]연속시간 푸리에 급수의 성질 (0) | 2022.07.06 |
| [푸리에급수]푸리에 급수의 계수 구하기 (0) | 2022.06.28 |
| [푸리에]푸리에를 들어가기 전 지수함수와 eigenfunction (0) | 2022.06.11 |



